UFRJ, Cálc.1, Listas do AVA, lista 17, 9
Um tronco de pirâmide com base quadrada de lado , topo quadrado de lado e altura . O que acontece se O que acontece se
Passo 1
Falaaaa, belezinha?? Bora lá para mais um probleminha dessa lista que tá quase no fim.
Primeiro, para entender o que precisamos para fazer essa questão, bora notar o seguinte:
Agora, vamos fazer um desenho só para entendermos quais serão os eixos e como trataremos o problema, bora checar que:
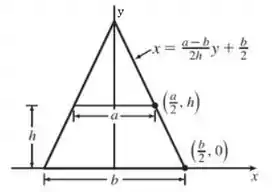
Essa é a visão da frente de toda a pirâmide, mas o que nos importa é apenas a parte até a altura .
Agora, precisamos entender quem é . Porém as seções serão quadrados de lado , para parte positiva do eixo e na outra parte, como nos eixos da figura.
Ou seja, temos que
Passo 2
Agora cabe a nós entendermos quem é em função dos carinhas que conhecemos. Na figura, já tá mostrando como faremos isso, será pela reta que está na figura. Porém temos que entender como chegar nessa reta.
Para calcular essa reta, faremos o seguinte:
Veja que a reta passa pelos pontos , além da reta passar pelo eixo no ponto , que será a interseção, ou seja:
Daí, temos que:
Passo 3
Agora basta fazermos a conta da integral e correr para o abraço:
Substituindo o valor de , temos:
Podemos cortar o :
Abrindo esse quadrado:
Dai, temos:
Ou seja, ficamos com:
E dai, substituindo:
Ajustando:
Colocando e em evidência:
Abrindo esse carinha, chegamos em:
Passo 4
Agora ele nos pede para analisar uns casos. Vamos notar que se temos um sólido retangular, com volume e se teremos uma pirâmide de base quadrada com volume , ou seja, tá tudo conforme o esperado.
E assim chegamos ao fim de outro probleminha, bora para o último?