Calcule o volume do sólido gerado pela rotação de
Em torno de .
Passo 1
Primeiro vou esboçar a região:
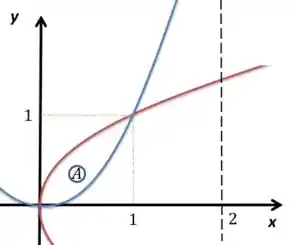
Bom, tenho que definir qual vai ser o meu raio de rotação nesse caso aí. Para o volume do sólido gerado na rotação do gráfico vermelho (, fica assim:
Pois, se é a distância do eixo até o gráfico e do eixo até a distância é , vale essa relação. Para o azul a mesma coisa:
Assim, o volume será dado pela resolução da integral:
Repara que com o giro em torno de uma reta paralela ao eixo eu integro em . Agora é conta.
Passo 2
Resposta
Exercícios de Livros Relacionados
Determine o volume do sólido obtido com a rotação da região limitada por y = x e pelas retas y = 2 e x = 0 em torno Do eixo x .Do eixo y .Da reta y = 2 .Da reta x = 4 .
Volume de um toro. O disco x 2 + y 2 ≤ a 2 gira em torno da reta x = b ( ba ) para gerar um sólido em forma de rosquinha chamado toro. Determine seu volume. (Sugestão: ∫ - a a a 2 - y 2 d y = π a 2 /
42: A região delimitada pelas curvas dadas é girada em torno do eixo especificado. Ache o volume do sólido resultante por qualquer método. x = y - 3 2 ,x = 4 ; em torno de y = 1 .
Por integração, determine o volume do sólido obtido pela rotação da região triangular com os vértices ( 0,0 ) , b , 0 e ( 0 , h ) em torno Do eixo x .Do eixo y .