Cálculo de Volumes através de Integrais
Considere a região do plano delimitada pela curva de equação e pela reta (eixo ).
- Calcule o volume do sólido gerado pela rotação de em torno da reta (eixo );
- Escreva uma integral que corresponda ao volume do sólido gerado pela rotação de em torno da reta . Não precisa calcular a integral.
Passo 1
Pelo método dos discos:
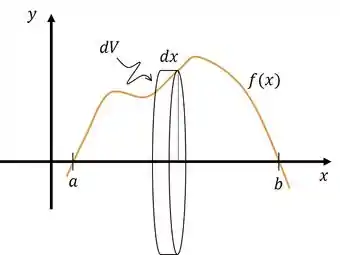
Somando todos os volumes infinitesimais desses disquinhos:
Sabemos que o raio é igual à altura do gráfico, ou seja, :
Passo 2
Agora precisamos saber onde a função encontra com o eixo para sabermos de onde até onde vai a nossa integral:
Cujas soluções são:
Portanto, nossa integral é no intervalo .
Passo 3
Resolvendo a integral, expandimos o quadrado perfeito:
E integramos termo à termo:
Substituindo os valores:
Passo 4
Vamos desenhar o que se pede:
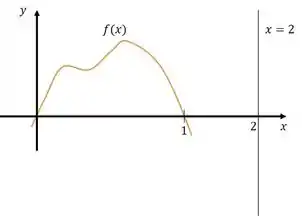
Girar em torno de um eixo paralelo à é bom pelo método das casca cilíndricas:
Onde é a distância de um ponto qualquer no eixo até a reta desejada. Um ponto qualquer no eixo tem equação:
Portanto a distância vai ser:
E a integral:
Resposta
a)
b)