UnB, Sem Campus, Cálculo 1, P3 - 2015.2, Questão 2
Com base na figura abaixo, determine a área da região ; e determine o volume do sólido gerado pela revolução de em torno do eixo .
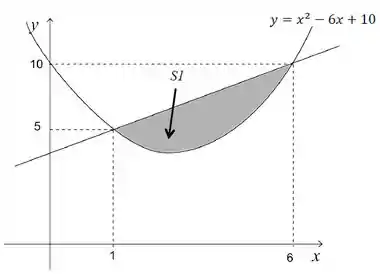
Passo 1
Fala, galera! Vamos resolver essa questão.
O enunciado pediu pra gente encontrar a área da região que é mostrada na figura e, em seguida, determinar o volume do sólido de revolução que é gerado na rotação dessa região em torno do eixo . Mas vamos por partes!
Pra determinar a área da região, a gente vai precisar olhar pra figura e ver que temos uma reta por cima da parábola , naquela região . Ele não nos disse qual é a função que define essa reta, mas ele nos deu dois pontos, e . A gente vai usar esses pontos pra calcular a equação geral da reta usando a fórmula:
Onde é o coeficiente angular da reta e é um ponto conhecido.
A partir disso, a gente pode usar a fórmula da área entre curvas pra calcular a área da região:
Em seguida, pra calcular o volume do sólido de revolução, nós vamos usar a equação:
Vamos lá!
Passo 2
Galera, vamos começar definindo a nossa reta. Primeira vamos calcular nosso coeficiente angular:
Onde e . Substituindo, temos:
E já podemos aplicar na equação da reta:
A gente usou o primeiro ponto pra calcular, mas qualquer um dos dois forneceria o mesmo resultado.
Passo 3
Agora que já sabemos que e , podemos calcular nossa área:
Repare que o gráfico já nos deu nosso intervalo de integração, que são os pontos onde as curvas se encontram. Assim,
E temos:
Integrando cada termo:
Aplicando os intervalos de integração em , temos:
Passo 4
Agora só falta a gente determinar o volume do sólido gerado pela revolução de em torno do eixo . Pra isso, nós vamos usar a equação:
Substituindo e , temos:
Abrindo esses produtos:
Integrando cada termo:
Agora só falta aplicar os limites de integração:
Prontinho, galera! Até a próxima! 😉