Faça um esboço da região do plano limitada pelas curvas e e pelas retas e . Expresse as grandezas abaixo utilizando integrais. Não é preciso calcular as integrais.
- A área de ;
- O volume do sólido de revolução obtido pela rotação de em torno do eixo .
Passo 1
(a)
Sempre bom dar uma visualizada no problema, então vamos começar esboçando a região .
O gráfico do seno de a é:
E o do cosseno:
Então a nossa região é assim:
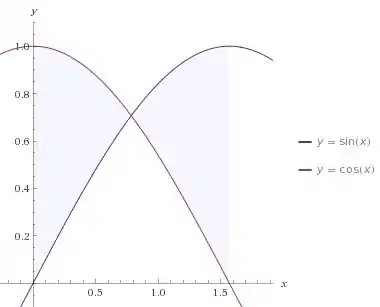
Passo 2
Repara que os gráficos se encontram bem no meio do intervalo, em , já que
Para , o gráfico do cosseno está em cima do gráfico do seno, e para , o seno é que está em cima.
Portanto, a área da região é dada por:
Passo 3
(b)
O volume sai pelo método dos anéis circulares.
A fórmula geral pra uma rotação em torno do eixo é
Então no nosso caso:
Resposta
(a)
(b)
Exercícios de Livros Relacionados
Determine o volume do sólido obtido com a rotação da região limitada por y = x e pelas retas y = 2 e x = 0 em torno Do eixo x .Do eixo y .Da reta y = 2 .Da reta x = 4 .
Volume de um toro. O disco x 2 + y 2 ≤ a 2 gira em torno da reta x = b ( ba ) para gerar um sólido em forma de rosquinha chamado toro. Determine seu volume. (Sugestão: ∫ - a a a 2 - y 2 d y = π a 2 /
42: A região delimitada pelas curvas dadas é girada em torno do eixo especificado. Ache o volume do sólido resultante por qualquer método. x = y - 3 2 ,x = 4 ; em torno de y = 1 .
Por integração, determine o volume do sólido obtido pela rotação da região triangular com os vértices ( 0,0 ) , b , 0 e ( 0 , h ) em torno Do eixo x .Do eixo y .