Cada integral representa o volume de um solido de revolução. Descreva a região que foi rotacionada e o eixo de rotação.
b.
Passo 1
Fala turminha, tudo em cima? Bora cair pra cima dessa questão! Primeiro, é importante saber que, a curva que vai ser rotacionada pra gerar nosso sólido, pode ser encontrada dentro da integral de revolução. Se liga na fórmula:
Portanto nosso é a equação dentro do parêntesis:
Passo 2
Boa, agora vamos desenhar essa parábola pra gente entender como vai ser nosso sólido de revolução. Vai ser mais tranquilo, porque nesse caso é uma parábola natural de concavidade para baixo (raízes -1 e 1), e que toca o eixo x no ponto 1. Portanto, temos o seguinte:
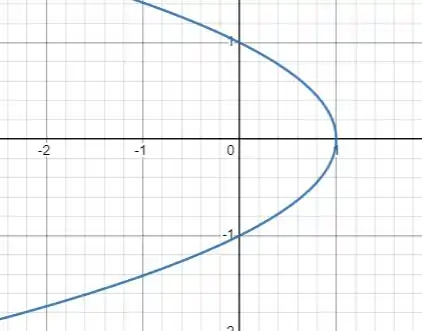
Passo 3
Perfeito. A revolução desse sólido, nos entrega algo parecido com uma bola de futebol americano, já que ela rotaciona em torno do eixo y (por conta do dy).