Calcule o volume do sólido produzido pela rotação de
ao redor do eixo .
Passo 1
O gráfico de é algo assim
E a região , é essa aqui
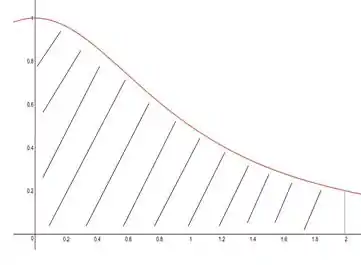
E vamos girar esse negócio em torno do eixo
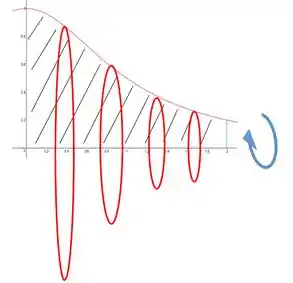
Passo 2
Pelo Método dos Discos Circulares, o volume do sólido produzido pela rotação de ao redor do eixo é dado pela integral:
Passo 3
Esse termo está pedindo pra gente usar a substituição trigonométrica:
Assim, usamos que
Adaptando os limites de integração:
Então a integral vai ficar:
Passo 4
Usando que:
Temos
Passo 5
Ainda podemos simplificar essa resposta! Usando a identidade trigonométrica
Calma que ainda não acabou, ainda dá pra simplificar isso...!
Passo 6
Digamos que , então
Isso nos diz que
Agora, usando a identidade trigonométrica
Ou seja:
Passo 7
Voltando pra nossa resposta:
Isso vai dar:
Resposta
Exercícios de Livros Relacionados
Determine o volume do sólido obtido com a rotação da região limitada por y = x e pelas retas y = 2 e x = 0 em torno Do eixo x .Do eixo y .Da reta y = 2 .Da reta x = 4 .
Volume de um toro. O disco x 2 + y 2 ≤ a 2 gira em torno da reta x = b ( ba ) para gerar um sólido em forma de rosquinha chamado toro. Determine seu volume. (Sugestão: ∫ - a a a 2 - y 2 d y = π a 2 /
42: A região delimitada pelas curvas dadas é girada em torno do eixo especificado. Ache o volume do sólido resultante por qualquer método. x = y - 3 2 ,x = 4 ; em torno de y = 1 .
Por integração, determine o volume do sólido obtido pela rotação da região triangular com os vértices ( 0,0 ) , b , 0 e ( 0 , h ) em torno Do eixo x .Do eixo y .