Determinar os volumes dos sólidos obtidos com a rotação das regiões sombreadas em torno dos eixos indicados.
c. 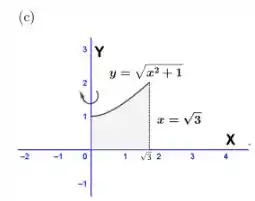
Passo 1
Fala turminha beleza? Bora lá! Pra essa questão de rotação de sólidos. Aqui, a grande jogada da questão é a gente calcular a diferença das integrais das equações que compõem o gráfico. Uma coisa que facilita nesse tipo de questão, é a gente imaginar como ficaria o sólido que a gente quer calcular. Aqui é como se fosse uma espécie de cilindro com uma furação cônica dentro.
Passo 2
Belezinha? Agora indo pros cálculos! Primeira coisinha que vamos fazer, é manipular o formato de , já que estamos rotacionando no eixo y. Portanto, vai ficar assim:
Show! Vamos armar nossa integral. Vamos montar primeiro uma integral do cilindro completo, e depois subtrair da integral que representa o volume do cone.
Passo 3
Por fim, pra gente finalizar a questão, precisamos achar os limites de integração. Pelo desenho, a gente sabe que os limites de integração são definidos por 0 e 2. E para a parte que representa o que vamo retirar, integraremos de 1 a 2, pois é a aonde o cone começa e termina. Isso porque é o intervalo que limita até aonde vamos no eixo y. Portanto, a integral que vamos resolver tem formato:
Resolvendo, a gente observa:
Logo,