Considere a região limitada pelas curvas e no intervalo .
- Esboce a região
- Calcule o volume do sólido gerado pela rotação de em torno do eixo .
Passo 1
a) Cara, para esboçar essa região , a gente precisa esboçar as curvas e no mesmo plano, e identificar a região que está entre elas no intervalo , beleza? E como a gente faz isso?
Nossas funções são:
Esperam da gente que saibamos a cara dessas funções (são chamadas de funções simples). A cara de é assim (uma reta que passa pela origem):
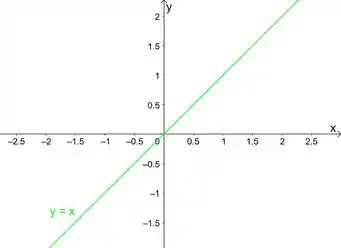
E é uma parábola que passa pela origem
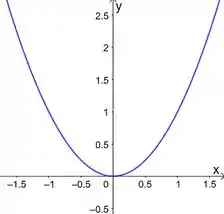
Colocando essas duas coisas no mesmo plano, e marcando a região entre elas no intervalo , achamos essa região aqui:
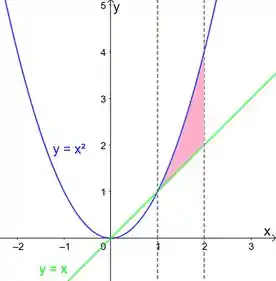
Passo 2
b) Para achar a o volume do sólido gerado pela rotação de em torno do eixo vamos usar o método dos anéis, porque temos um intervalo bem definido em , também é nosso eixo de rotação e temos funções de .
Nesse método, a gente precisa montar a fórmulinha:
A representa a função que limita a nossa região por cima, e a função que limita a nossa região por baixo.
Olhando ali no nosso desenho, vemos que quem limita nossa região por cima é a e quem limita nossa região por baixo é a função .
Aí a gente tem que para o nosso caso:
E na fórmula, é o intervalo em que nossa região está. Do enunciado temos que nossa região está no intervalo , então:
E aí a nossa integral para calcular o volume fica:
Repara que a gente simplificou ali nossa função usando uma propriedade de potência.
Passo 3
Agora é calcular essa belezura. Uma propriedade diz que podemos fazer a integral de cada uma das funções e depois fazer a subtração:
Percebe que nessas duas integrais, a gente pode usar a regrinha:
Para a primeira integral temos e para a segunda temos . Ficamos assim então:
Resposta
a) 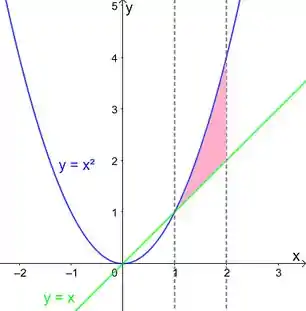
b)