Um fabricante de móveis em madeira produz pés de apoio para móveis a partir de blocos de madeira que serão torneados por uma serra de fita que segue o traçado de uma curva determinada por , de até .
Os pés de apoio são obtidos quando a região sob a curva é girada em torno do eixo . Encontre o volume de cada pé de apoio produzido por este método.
(a)
(b)
(c)
(d)
(e)
Passo 1
Estamos tomando essa área aqui:
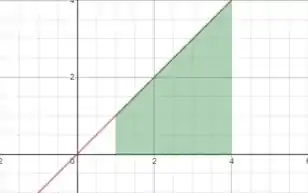
E girando em torno do eixo para formar um volume. Existe uma fórmula para esse caso:
Agora é só resolver essa integral:
Passo 2
Como a integral de é , se substituirmos os limites de integração:
Pronto!
Resposta
Letra (c).