Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Cálculo de Volumes – Discos e Anéis

Ver Teoria
Exercício 106123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

UFSC – Cálculo C – P1 – Questão 4-Parte II (adaptado)

Calcule o volume da região de intersecção de x 2 + y 2 + z 2 ≤ 4 com x 2 + y 2 ≤ 2 x .

Passo 1

E aí pessoal, tudo bem? O problema nos deu essas duas equações aqui

x 2 + y 2 + z 2 ≤ 4

x 2 + y 2 ≤ 2 x  

E pediu para não só calcular o volume entre as duas curvas, como também esboçar a região de intersecção.

A resolução ficaria pouco longa, então resolvi dividir em duas partes: na primeira parte (i) fizemos o esboço dessa região, para entender como essas curvas estão dispostas no espaço. Já na parte (ii) vamos calcular o volume! Beleza?

Na primeira parte esboçamos a região de intersecção, encontramos esses limites de integração

- 4 - r 2 < z < 4 - r 2

2 c o s θ < r < 2

0 < θ < 2 π

E o esboço foi esse aqui:

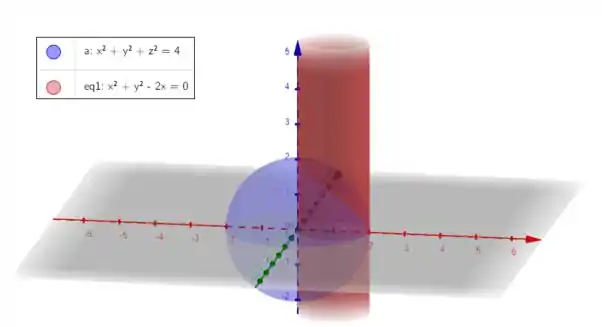
Agora o problema pede para calcularmos o volume!

Então a ideia é: com os limites já definidos, montar a integral e ir resolvendo aos poucos! Mas aqui temos uma ajudinha: como temos uma região simétrica (vai de raiz até raiz em z ), podemos fazer de 0 até a raiz e multiplicar por dois! E em θ também! Podemos multiplicar por 4 e ir de 0 até π 2

Mas relaxa, vou fazer passo a passo com você!

Passo 2

Nossos limites são

- 4 - r 2 < z < 4 - r 2

2 c o s θ < r < 2

0 < θ < π / 2

Estamos em coordenadas cilíndricas, então nosso diferencial de volume fica assim

d V = r   d z   d r   d θ

Aí nossa integral fica assim

8 ∫ 0 π / 4 ∫ 2 c o s θ 2 ∫ 0 4 - r 2 r   d z   d r   d θ

Tranquilo até aqui?

Agora nossa missão é integrar essa coisa!

Passo 3

Primeiro em z :

8 ∫ 0 π / 2 ∫ 2 c o s θ 2 ∫ 0 4 - r 2 r   d z   d r   d θ = 8 ∫ 0 π / 2 ∫ 2 c o s θ 2 r   z 0 4 - r 2 d r   d θ

8 ∫ 0 π / 2 ∫ 2 c o s θ 2 r   4 - r 2 d r   d θ

Tudo bem? Agora vamos integrar em r , usando substituição simples

8 ∫ 0 π / 2 - 1 2 . 2 3 4 - r 2 2 c o s θ 3 2 d θ = - 8 3 ∫ 0 π / 2 0 - 4 - 4 cos 2 ⁡ θ 3 2 d θ = 8 3 ∫ 0 π / 2 4 3 2 1 - cos 2 ⁡ θ 3 / 2 d θ

Tudo bem até aqui?

Agora vamos usar a identidade trigonométrica s e n 2 θ = 1 - cos 2 ⁡ θ   e integrar em θ

= 8 3 . 8 ∫ 0 π / 2 s e n θ s e n 2 θ d θ = 64 3 ∫ 0 π / 2 s e n θ 1 - cos 2 ⁡ θ d θ

Podemos separar em duas integrais

64 3 ∫ 0 π / 2 s e n θ d θ - 64 3 ∫ 0 π / 2 s e n θ cos 2 ⁡ θ d θ = 64 3 - c o s θ 0 π 2 + 64 3 cos 3 ⁡ θ 3 0 π / 2

Beleza? E por fim aplicar nos limites

64 3 - 0 + 1 + 64 3 0 - 1 3 = 64 3   . 2 3 = 128 9

E é isso!

Espero ter ajudado! Vamos para a próxima?

Resposta

128 9

Exercícios de Livros Relacionados

Determine o volume do sólido obtido com a rotação da região limitada por y = x e pelas retas y = 2 e x = 0 em torno Do eixo x .Do eixo y .Da reta y = 2 .Da reta x = 4 .
Volume de um toro. O disco x 2 + y 2 ≤ a 2 gira em torno da reta x = b ( ba ) para gerar um sólido em forma de rosquinha chamado toro. Determine seu volume. (Sugestão: ∫ - a a a 2 - y 2 d y = π a 2 /
42: A região delimitada pelas curvas dadas é girada em torno do eixo especificado. Ache o volume do sólido resultante por qualquer método. x = y - 3 2 ,x = 4 ; em torno de y = 1 .
Por integração, determine o volume do sólido obtido pela rotação da região triangular com os vértices ( 0,0 ) , b , 0 e ( 0 , h ) em torno Do eixo x .Do eixo y .