Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Cálculo de Volumes – Discos e Anéis

Ver Teoria
Exercício 251234567891011121314151617181920212223242627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Cálculo de Volumes através de Integrais

Um objeto é esculpido a partir de um tronco cilíndrico de madeira maciça com diâmetro de 2 L metros e comprimento de 4 metros. O objeto tem a forma do sólido de revolução obtido pela rotação, em torno do eixo x , da região limitada pela curva y = L 2 x 2 + x , x   ϵ   [ 1,5 ] , e pelo eixo x . Calcule o volume de madeira desperdiçado.

Passo 1

Esquematizando esse corte no tronco, dadas as dimensões, fica mais ou menos assim:

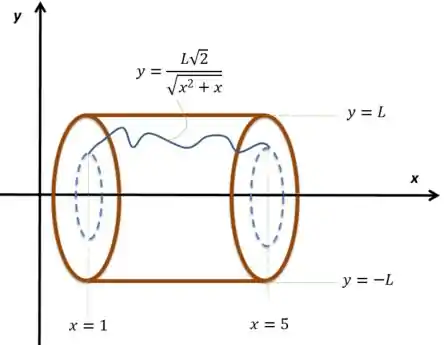
Repara que essa linha em azul é a função que eu vou rotacionar. Eu sinceramente nem me importo muito sobre como ela vai ser, já que eu sei pela própria função que ela é contínua entre x = 1 e x = 5 além de que ela também é sempre positiva nesse espaço. Daí, amigo, basta a gente se dar conta que o volume desperdiçado é o volume total do tronco original (que é um cilindro) menos o volume rotacionado da função aí.

Por partes, olhando primeiro para o cilindro total, o volume sai por fórmula:

V T r o n c o = π r 2 h = π L 2 5 - 1 = 4 π L 2

Agora basta calcular o volume por seções transversais.

Passo 2

A integral é aquela que a gente já conhece, aplicando corretamente os limites dados no enunciado e a função:

V = ∫ a b π f x 2 d x = ∫ 1 5 π L 2 x 2 + x 2 d x

= ∫ 1 5 π 2 L 2 x 2 + x d x = 2 L 2 π ∫ 1 5 1 x 2 + x d x

Repara que esse x 2 + x pode ser aberto como x ( x + 1 ) , o que aparenta ser fácil de fazer por frações parciais! Vou abrir a função em dois quocientes então e aí integramos.

1 x 2 + x = A x + B x + 1 = A + B x + A x 2 + x

A = 1 A + B = 0

A = 1 ; B = - 1

Portanto, nossa integral se resume a essa aqui:

2 L 2 π ∫ 1 5 1 x 2 + x d x = 2 L 2 π ∫ 1 5 1 x - 1 x + 1 d x

= 2 L 2 π ln ⁡ x - ln ⁡ x + 1 [ 5 1

= 2 L 2 π ln ⁡ x x + 1 [ 5 1

= 2 L 2 π ln ⁡ 5 5 + 1 - ln ⁡ 1 1 + 1

= 2 L 2 π ln ⁡ 5 6 - ln ⁡ 1 2 = 2 L 2 π ln ⁡ 5 6 1 2 = 2 L 2 π ln ⁡ 5 3

Passo 3

Ok, sabemos enfim qual será o volume desperdiçado

V d i s p e r d i ç a d o = 4 π L 2 - 2 L 2 π ln ⁡ 5 3

= π L 2 4 - 2 ln ⁡ 5 3   m 3

Resposta

V = π L 2 4 - 2 ln ⁡ 5 3   m 3

Exercícios de Livros Relacionados

Determine o volume do sólido obtido com a rotação da região limitada por y = x e pelas retas y = 2 e x = 0 em torno Do eixo x .Do eixo y .Da reta y = 2 .Da reta x = 4 .
Volume de um toro. O disco x 2 + y 2 ≤ a 2 gira em torno da reta x = b ( ba ) para gerar um sólido em forma de rosquinha chamado toro. Determine seu volume. (Sugestão: ∫ - a a a 2 - y 2 d y = π a 2 /
42: A região delimitada pelas curvas dadas é girada em torno do eixo especificado. Ache o volume do sólido resultante por qualquer método. x = y - 3 2 ,x = 4 ; em torno de y = 1 .
Por integração, determine o volume do sólido obtido pela rotação da região triangular com os vértices ( 0,0 ) , b , 0 e ( 0 , h ) em torno Do eixo x .Do eixo y .