USP, Sem Campus, Cálculo 1, Listas de Cálculo 1 - USP - Lista 2, Questão 5.10
Calcule o volume de uma calota esférica de altura , , de uma esfera de raio .
Passo 1
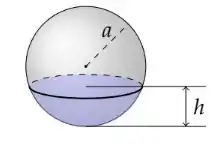
Eaee!!! Belezinha? Bom... a questão quer que a gente calcule o volume da seguinte calota esférica de altura e raio :
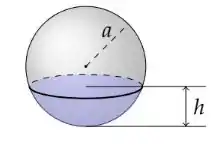
Para isso, a calota esférica pode ser pensada como uma série de fatias infinitesimais, cada uma delas sendo um anel perpendicular ao eixo da calota.
Assim, para calcular o volume, vamos integrar essas fatias!!
Agora vamos juntos!!
😉
Passo 2
Então... Vamos considerar um anel infinitesimal à distância do vértice da calota. A área da seção transversal desse anel é:
Onde é a espessura infinitesimal do anel.
O raio do anel é o raio da esfera maior menos a distância , ou seja:
Agora, podemos calcular o volume infinitesimal dessa fatia:
Passo 3
Agora, integrando ambos os lados, podemos encontrar o volume da calota:
Entendeu direitinho? Responde aee ;)
