Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Cálculo de Volumes – Discos e Anéis

Ver Teoria
Exercício 151234567891011121314161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

UFCG. Cálculo Diferencial e Integral II. Listas de Cálculo 2 UAMat. Lista 3. Questão 3a.

3 - Determine o volume dos sólidos obtidos com a rotação, em torno do eixo x , da região limitada pelas curvas:

(a) y = x 2 , y = 0 , x = 2 .

Passo 1

Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉

Nesse problema temos que o volume do solido formado pela rotação da região limitada pelas curvas y = x 2 , y = 0 e x = 2 em torno do eixo x .

A primeira coisa que temos que obter é a região no plano x y que vamos revolucionar em x .

Esboçando as curvas y = x 2 , y = 0 , x = 2 no plano e hachurando a região entre elas, vamos obter

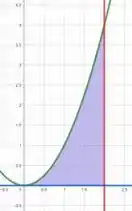
Mas então como vamos obter o volume do solido que se forma? 🤔🤔

Para obter o volume do solido, podemos usar o método dos discos. Esse método consiste em dividir o solido em discos de alturas infinitesimais.

Bora ver como fazemos isso? 😉

Passo 2

A altura do nosso sólido é representada pelo eixo x e o raio dos discos infinitesimais pela distância de y = 0 até a curva y = x 2

Se o volume de um disco é dado por

V = π r 2 h

Então cada volume infinitesimal d V é dado substituindo r por y = x 2 e h por uma altura infinitesimal d x , ou seja

d V = π x 2 2 d x

d V = π x 4 d x

Integrando dos dois lados, temos

∫ d V = ∫ π x 4 d x

V = ∫ π x 4 d x

Estamos interessados apenas no volume que se forma entre x = 0 e x = 2 , então vamos usar esses valores como limites de integração.

V = ∫ 0 2 π x 4 d x

Tranquilo até aqui? 😎

Passo 3

Agora finalmente podemos resolver a integral que vai nos obter o volume do sólido!

Como π é uma constante podemos colocá-la fora da integral.

V = π ∫ 0 2 x 4 d x

Integrando pelo método de integração polinomial somando 1 no expoente da variável e a dividindo pelo resultado dessa soma, temos

∫ x 4 d x = x 4 + 1 4 + 1 = x 5 5

Aplicando os limites de integração

∫ 0 2 x 4 d x = 2 5 5 - 0 5 5

∫ 0 2 x 4 d x = 32 5

Substituindo em V , temos

V = π ∫ 0 2 x 4 d x

V = 32 π 5

Portanto, o volume do solido formado pela revolução da região que tínhamos no passo 1 é 32 π 5 .

É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍

Resposta

V = 32 π 5

Exercícios de Livros Relacionados

Determine o volume do sólido obtido com a rotação da região limitada por y = x e pelas retas y = 2 e x = 0 em torno Do eixo x .Do eixo y .Da reta y = 2 .Da reta x = 4 .
Volume de um toro. O disco x 2 + y 2 ≤ a 2 gira em torno da reta x = b ( ba ) para gerar um sólido em forma de rosquinha chamado toro. Determine seu volume. (Sugestão: ∫ - a a a 2 - y 2 d y = π a 2 /
42: A região delimitada pelas curvas dadas é girada em torno do eixo especificado. Ache o volume do sólido resultante por qualquer método. x = y - 3 2 ,x = 4 ; em torno de y = 1 .
Por integração, determine o volume do sólido obtido pela rotação da região triangular com os vértices ( 0,0 ) , b , 0 e ( 0 , h ) em torno Do eixo x .Do eixo y .