UFCG – Sem Campus – Cálculo Diferencial e Integral II – Listas de Cálculo 2 – UAMat – Lista 3 – Questão 5d
Determine o volume do sólido obtido com a rotação, em torno do eixo , das regiões limitadas pelas retas e curvas:
d)
Passo 1
Faaala gente bonita, tudo certinho?
Nesse exercício precisamos calcular o volume de um sólido obtido quando rotacionamos, em torno do eixo , a região delimitada pelas curvas:
Mas, antes de tudo, vocês lembram algum método que podemos usar pra calcular volume de sólido obtido por rotação?
Tem um método bem legal, que ajuda bastante quando queremos rotacionar uma região em torno do eixo , é o método dos discos. Segundo ele:
Então, vamos inicialmente identificar essa região no plano , e depois aplicamos o método dos discos pra obter o volume de rotação, beleza?
Passo 2
Bom, a nossa região é delimitada pelas curvas:
A primeira curva é uma parábola, ela tem sua concavidade para baixo. Suas raízes são:
Massa! Assim, temos a seguinte curva:
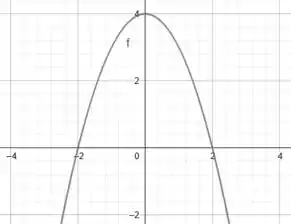
Show!
Já na nossa segunda curva temos a equação de uma reta. Para desenhá-la basta identificarmos dois pontos. Fazendo e , temos e , respectivamente. Ligando os pontos, e colocando as duas curvas em um gráfico:
Prontinho! A região entre as duas curvas é justamente a nossa região que será rotacionada?
Tranquilo até aqui?
Passo 3
Boa galera! Agora que já identificamos a região que será rotacionada, vamos pensar em como aplicar o nosso método dos discos aqui.
Um ponto importante desse método, é que quando fazemos:
Estamos calculando o volume obtido quando rotacionamos a região abaixo da curva em torno do eixo . Mas, a nossa região de integração é:
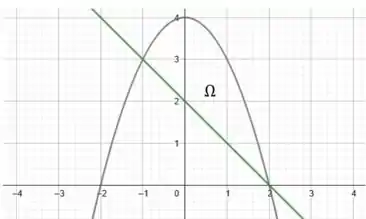
Assim, para calculá-la precisamos fazer uma pequena operação entre as áreas abaixo da curva cinza e da curva verde.
Podemos dizer que:
onde:
É o volume do sólido obtido pela rotação da curva cinza .
É o volume do sólido obtido pela rotação da curva verde .
Massa! Agora precisamos apenas determinar os limites de integração que envolvem a nossa região . Basicamente, eles resultam da intersecção das duas curvas. Assim, para calculá-los, fazemos:
Cujas raízes podemos obter por inspeção, sendo elas e . Portanto, agora é só montarmos as integrais.
Para :
Para :
Perfeito!
Passo 4
Agora é só nós calcularmos as integrais!
Colocando para fora da integral (já que é uma constante), e elevando o integrando ao quadrado:
Lembrando da regra da integração de monômios:
Daí:
Aplicando os limites de integração:
Por fim:
Vamos agora para
Colocando as constantes para fora, e elevando o integrando ao quadrado:
Usando a mesma regra de integração de :
Logo:
Portanto, retomando a equação que chegamos no passo para :
Ufaaa! Terminamos. É isso gente, obrigado pela atenção. Até a próxima 😊