Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Cálculo de Volumes – Discos e Anéis

Ver Teoria
Exercício 691234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768707172737475767778798081828384858687888990919293949596979899100

Enunciado

UFSCAR – Cálculo 1 – SUB – Questão 3

Determine o volume do sólido S obtido pela rotação em torno do eixo x da região delimitada pelas retas x = 0 ; x = 1 ; e pelos gráficos das funções f x = x e g x = 3 .

Passo 1

Oi, tudo bem? O problema deu duas funções

f x = x

g x = 3

E pediu para calcularmos o sólido de revolução formado pela área compreendida por essas duas funções, e mais essas curvas aqui

x = 0

x = 1

Mas você lembra como encontrar?

A primeira coisa que vamos fazer é determinar qual é a região que estamos lidando! E isso porque o volume de um sólido de revolução é dado por

V = π ∫ a b f x 2 - g x 2 d x

É como se fosse o volume de uma rosquinha! Mas agora com os raios como funções: a função mais de fora menos a mais de dentro

Então para achar o volume precisamos encontrar a região e verificar se temos um volume ‘vazado’ ou não.

ok?

Mas relaxa, vou fazer com você!

Passo 2

Vamos começar esboçando o gráfico:

f x = x

g x = 3

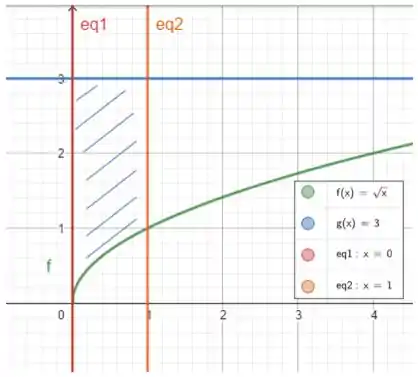E as retas verticais

x = 0

x = 1

Vemos que a função que está mais em cima é g x = 3 e a que está por baixo f x = x . E os limites de integração? A gente vê que em x

0 < x < 1

O volume vai ser de uma tigela! Olha só:

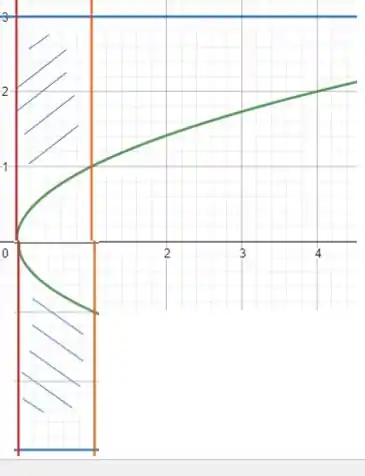
É um espelhamento em torno do eixo x ! Aí nossa integral de volume vai ficar

V = π ∫ 0 1 3 2 - x 2 d x

Agora é “só” resolver!

Passo 3

Nosso volume é

V = π ∫ 0 1 3 2 - x 2 d x

Simplificando o integrando temos

V = π ∫ 0 1 9 - x d x

Agora é só aplicar as regras de integração que conhecemos!

V = π 9 - x 2 2 0 1  

E aplicar nos limites de integração

V = π 9 - 1 2 = 17 π 2

Oba! Terminamos!

Espero ter ajudado! Vamos para a próxima?

Resposta

17 π 2

Exercícios de Livros Relacionados

Determine o volume do sólido obtido com a rotação da região limitada por y = x e pelas retas y = 2 e x = 0 em torno Do eixo x .Do eixo y .Da reta y = 2 .Da reta x = 4 .
Volume de um toro. O disco x 2 + y 2 ≤ a 2 gira em torno da reta x = b ( ba ) para gerar um sólido em forma de rosquinha chamado toro. Determine seu volume. (Sugestão: ∫ - a a a 2 - y 2 d y = π a 2 /
42: A região delimitada pelas curvas dadas é girada em torno do eixo especificado. Ache o volume do sólido resultante por qualquer método. x = y - 3 2 ,x = 4 ; em torno de y = 1 .
Por integração, determine o volume do sólido obtido pela rotação da região triangular com os vértices ( 0,0 ) , b , 0 e ( 0 , h ) em torno Do eixo x .Do eixo y .