Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Cálculo de Volumes – Discos e Anéis

Ver Teoria
Exercício 104123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Determinar os volumes dos sólidos obtidos com a rotação das regiões sombreadas em torno dos eixos indicados.

d.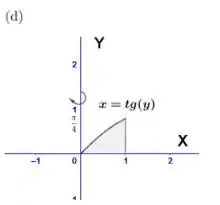

Passo 1

Fala turminha beleza? Bora lá! Pra essa questão de rotação de sólidos. Aqui, a grande jogada da questão é a gente calcular a diferença das integrais das equações que compõem o gráfico. Uma coisa que facilita nesse tipo de questão, é a gente imaginar como ficaria o sólido que a gente quer calcular. Aqui é como se fosse uma espécie de cilindro com uma furação cônica dentro.

Passo 2

Belezinha? Agora indo pros cálculos! Vamos armar nossa integral. Vamos montar primeiro uma integral do cilindro completo, e depois subtrair da integral que representa o volume do cone.

V s = V c - V i

V s = π ∫ x 2   d y - ∫ t g   y   d y

Passo 3

Falando agora de limite de integração, vamos limitar até aonde nosso cilindro é projetado no eixo y, ou seja, até π 4 . Mas ora, sabemos que o valor de x = 1 , pela limitação dele no eixo x.

Logo, nossa integral vai ficar assim:

V s = V c - V i

V s = π ∫ 0 π 4 x 2   d y - π ∫ 0 π 4 t g   y   d y    

Resolvendo:

V S = π ⋅ 1 2 ⋅ y   ​ 0 π 4 - π t g   y ​ 0 π 4

V s = π π - 2 2

Resposta

V s = π π - 2 2

Exercícios de Livros Relacionados

Determine o volume do sólido obtido com a rotação da região limitada por y = x e pelas retas y = 2 e x = 0 em torno Do eixo x .Do eixo y .Da reta y = 2 .Da reta x = 4 .
Volume de um toro. O disco x 2 + y 2 ≤ a 2 gira em torno da reta x = b ( ba ) para gerar um sólido em forma de rosquinha chamado toro. Determine seu volume. (Sugestão: ∫ - a a a 2 - y 2 d y = π a 2 /
42: A região delimitada pelas curvas dadas é girada em torno do eixo especificado. Ache o volume do sólido resultante por qualquer método. x = y - 3 2 ,x = 4 ; em torno de y = 1 .
Por integração, determine o volume do sólido obtido pela rotação da região triangular com os vértices ( 0,0 ) , b , 0 e ( 0 , h ) em torno Do eixo x .Do eixo y .