UFCG – Sem Campus – Cálculo Diferencial e Integral II – Listas de Cálculo 2 – UAMat – Lista 3 – Questão 5c
Determine o volume do sólido obtido com a rotação, em torno do eixo , das regiões limitadas pelas retas e curvas:
c)
Passo 1
Eaai gente, tudo tranquilo?
Nesse exercício, temos uma região no plano que é limitada pelas curvas:
Essa região é rotacionada em torno do eixo gerando um sólido. Queremos determinar o volume desse sólido de revolução. Sacou?
Bom, com certeza vamos precisar entender melhor quem é essa região que será rotacionada. Mas, principalmente, precisamos lembrar alguma forma de calcular volume de sólidos de revolução. Vocês lembram?
Tem um método legal de utilizar nos casos de rotação em torno do eixo x. É o método dos discos, segundo ele:
Então, vamos lá! Primeiro identificamos quem é nossa região, depois montamos e calculamos essa integral.
Passo 2
Pra identificar nossa região, vamos pensar nas curvas que as formam.
A primeira curva é uma parábola, que não possui raízes reais, pois:
Assim, a parábola está acima do eixo . Como podemos ver:
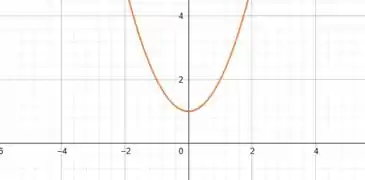
Já a segunda curva é uma reta, cuja equação vale:
Para desenhá-la, basta identificarmos dois pontos. Por exemplo, e . Assim, juntando ambas as curvas em um gráfico:
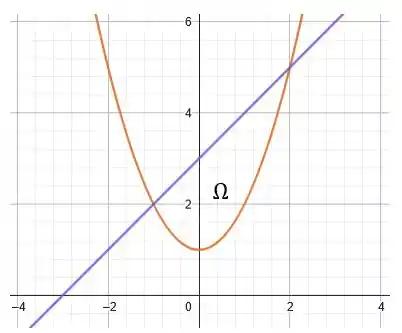
Ou seja, é justamente a região entre as duas curvas, .
Massa!
Passo 3
Agora vamos montar as integrais.
Antes de começarmos, é importante entender que o método dos discos, calcular o volume obtido pela rotação de uma região abaixo da curva
Assim, para calcularmos o volume obtido pela rotação de por esse método, precisamos fazer uma operação entre volumes. Podemos dizer que:
onde:
é o volume obtido pela rotação da região abaixo de no intervalo em que se encontra.
é o volume obtido pela rotação da região abaixo de no intervalo em que se encontra.
Pegaram a ideia?
Para montarmos as integrais correspondentes a esses volumes falta apenas determinarmos os limites de integração.
É justamente o intervalo de valores de que delimitam nossa região . Ou seja, está entre os dois pontos de intersecção entre as duas curvas.
Fazendo:
Temos:
Por inspeção, vemos que e são raízes. Portanto, nosso intervalo de integração vai de a , beleza?!
Lembrando que:
Temos:
Onde o primeiro termo é e o segundo é .
Passo 4
Agora vamos calcular as integrais. Começando por :
Colocando pra fora da integral e elevando o integrando ao quadrado, ficamos com:
Como a integral da soma é a soma das integrais:
Lembrando também da regra de integral de monômios:
Vamos ter:
Logo:
Perfeito!
Calculando , temos:
Novamente colocando para fora e elevando o integrando ao quadrado:
Usando a regra de integração de polinômios:
Logo:
Pra finalizar, basta usar que:
Por fim:
Eaí, curtiram a solução? Responde aí!