Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Cálculo de Volumes – Discos e Anéis

Ver Teoria
Exercício 621234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606163646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Determine o volume do sólido obtido pela rotação, em torno do eixo x , da região R , situada no primeiro quadrante, limitada pelas retas x = 2 e y = 0 e pelas curvas y = x ² e y = x - 1 .

Passo 1

A parábola y = x ² tem concavidade para cima e raiz única em x = 0 . Portanto, a partir desse ponto ela cresce infinitamente. Já a curva y = x - 1 intercepta o eixo x em x = 1 e a partir desse ponto também cresce infinitamente. No entanto, o crescimento de y = x - 1 é menor que o crescimento de y = x ² . Com isso e as informações dadas pelo enunciado, o esboço da região a ser rotacionada é o seguinte:

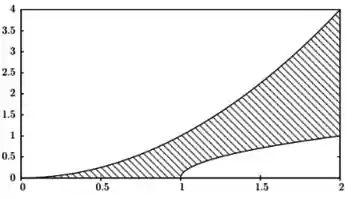
Passo 2

A área hachurada será obtida pela subtração da área gerada pela rotação da parábola pela área gerada pela rotação de   x - 1 . O intervalo de rotação da parábola vai de x = 0 a x = 2 . Já o intervalo de rotação de x - 1 vai de x = 1 a x = 2 . O Volume pode ser dado, então pela seguinte expressão:

V = ∫ 0 2 π x 2 2 d x - ∫ 1 2 π x - 1 2 d x

V = ∫ 0 2 π x 4 d x - ∫ 1 2 π ( x - 1 ) d x

V = π ∫ 0 2 x 4 d x - π ∫ 1 2 x - 1   d x

V = π x 5 5 0 2 - π x 2 2 - x 1 2

V = π 2 5 5 - 0 - π 2 2 2 - 2 - 1 2 2 - 1

V = π 32 5 - π 0 - - 1 2

V = π 32 5 - π 1 2

V = 32 π 5 - π 2

Resposta

V = 32 π 5 - π 2

Exercícios de Livros Relacionados

Determine o volume do sólido obtido com a rotação da região limitada por y = x e pelas retas y = 2 e x = 0 em torno Do eixo x .Do eixo y .Da reta y = 2 .Da reta x = 4 .
Volume de um toro. O disco x 2 + y 2 ≤ a 2 gira em torno da reta x = b ( ba ) para gerar um sólido em forma de rosquinha chamado toro. Determine seu volume. (Sugestão: ∫ - a a a 2 - y 2 d y = π a 2 /
42: A região delimitada pelas curvas dadas é girada em torno do eixo especificado. Ache o volume do sólido resultante por qualquer método. x = y - 3 2 ,x = 4 ; em torno de y = 1 .
Por integração, determine o volume do sólido obtido pela rotação da região triangular com os vértices ( 0,0 ) , b , 0 e ( 0 , h ) em torno Do eixo x .Do eixo y .