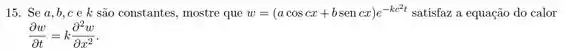
Passo 1
Bora lá calcular as derivadas parciais disso aí né..
Começando pela derivada parcial em relação a .
Pela regra da cadeia:
Arrumando só pra ficar bonitinho (ou menos feio):
Passo 2
Agora derivada parcial em relação a .
Usando a regra da cadeia:
Agora arrumando:
Passo 3
Agora a gente deriva isso de novo em relação a , porque a equação o enunciado envolve derivada segunda de .
Arrumando:
Passo 4
Agra, de acordo com o enunciado, devemos ter
Substituindo as derivadas que a gente achou
Organizando melhor isso:
Vemos que os dois lados são iguais, ou seja, provamos que a expressão do enunciado é verdadeira.
Resposta
Exercícios de Livros Relacionados
Encontrar a inclinação da reta tangente à curva resultante da intersecção de z = f ( x , y ) com o plano x = x 0 no ponto P ( x 0 , y 0 ,z 0 ) .a) z = x 2 + y 2 - 1 ; P ( 1 ,- 1 ,1 )
Mostre que a função produção de Cobb-Douglas satisfaz P L , K 0 = C 1 K 0 L α resolvendo a equação diferencial d P d L = α P L
No estudo de penetração do congelamento descobriu-se que a temperatura T no instante t (medido em dias) a uma profundidade x (medida em pés) pode ser modelada pela função T ( x , t ) = T 0 + T 1 e - λ
80. A temperatura em um ponto x ,y de uma chapa de metal é dada por T x ,y = 60 / ( 1 + x 2 + y 2 ) , onde T é medido em ° C e x , y em metros. Determine a taxa de variação da temperatura no ponto 1 ,
Seja ϕ : R → R uma função diferenciável tal que ϕ ' 3 = 4 . Seja g x , y , z = ϕ x 2 + y 2 + z 2 . Calcule:a) ∂ g ∂ x 1,1 , 1 b) ∂ g ∂ y 1,1 , 1 c) ∂ g ∂ z 1,1 , 1