UFABC. Cálculo. Funções de Várias Variáveis. Lista 5 - Pontos Críticos, Máximos e Mínimos, Multiplicadores de Lagrange. Questão 11.
11 - Numa circunferência de raio , traçam-se duas cordas paralelas, uma acima e outra abaixo do centro, e constrói-se um trapézio isósceles. Determine as distâncias das duas cordas ao centro para que a área do trapézio seja máxima.
Passo 1
Iae, como vai? Essa questão está um pouco complicada? Fique tranquilo que vamos tentar te ajudar. 😎👍
Nessa questão temos uma circunferência de raio e temos duas cordas pra passar uma abaixo e outra a cima do centro da circunferência. Ligando os dois pontos de cada lado onde a corda se encontra com a circunferência, vamos ter um trapézio, veja só
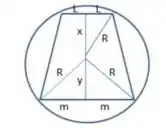
A ideia é calcular os valores das distancias das cordas até o centro em que a área do trapézio seja a máxima, ou seja, vamos calcular os valores de e .
Minha nossa!! Como vamos fazer isso?? 🤔🤔
Relaxa, vamos encontrar a função que descreve a área em função de e , veja só!
Passo 2
Com base na imagem, podemos definir dois triângulo-retângulos no trapézio
Vamos isolar e em um lado da igualdade para ver o que vamos obter
Lembra como é a fórmula de área do trapézio?
O que é a base maior? , não é?
E a base menor? , certo?
E a altura ? , ok?
Vamos substituir esses valores na formula da área
Acabamos de encontrar e , não é? Vamos substituir na equação de .
Como calculamos o maior valor para uma função? Derivamos e igualamos a para encontrar os pontos críticos! Isso aí!
Passo 3
Nesse caso, vamos derivar aplicando a regra do produto e a regra da cadeia, olhe só.
Temos a multiplicação de duas funções, consegue ver?
Então a derivada de é dada pela derivada da primeira · a segunda + a primeira · a derivada da segunda, ou seja
Mas perceba que na derivada da primeira, vamos usar a regra da cadeia pois temos uma função composta. Com isso a regra da cadeia nos diz que a derivada de uma função composta é dada pela derivada de dentro · derivada de fora. Entendeu? Vai ficar claro na prática.
Primeiro vamos derivar com relação a .
Pela regra da cadeia na derivada de fora, a função de dentro é substituída por uma constante, veja só.
A derivada de é igual a então podemos desconsiderar quando derivamos em .
Substituindo em
Todas as derivadas podem ser obtidas por derivada de polinômios, onde multiplicamos a variável pela potência e subtraímos do expoente.
Tranquilo até aqui? 👀
Passo 4
Vamos calcular essas derivadas
Substituindo por de volta, temos
Substituindo esses resultados, temos
Simplificando o resultado, temos
Pelo mesmo método, vamos obter a derivada de com relação a
Podemos ver que a aplicação da regra da cadeia na primeira derivada é muito parecida, logo
Bora resolver essas derivadas? 😁
Passo 5
Pelo método de derivação de polinômios e pelo que já calculamos anteriormente no caso de , temos
Substituindo esses resultados na nossa derivada, temos
Igualando e a , temos um sistema de equações dadas por
Podemos afirmar que
Se essa igualdade é verdadeira, podemos dizer que
Simplificando
Interessante, não é?
Passo 6
A primeira relação que podemos fazer é que , veja como as duas frações são idênticas, se diferenciando apenas por e . Se manipularmos uma pouco mais essa equação, podemos provar isso, mas no caso, a visualização é suficiente.
Vamos isolar
Com isso, vamos substituir
Manipulando essa equação, vamos simplificar o resultado
Com isso, obrigatoriamente o numerador deve ser igual a
E também se , podemos dizer que
Vamos desenvolver essa equação.
Passo 7
veja só a mágica que podemos fazer agora!
Vamos colocar em evidência
Como não pode ser , só podemos ter
Isolando em um lado da igualdade, temos
Tirando a raiz dos dois lados, vamos obter
Como vimos que , logo
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí
