Considere as afirmações abaixo e marque verdadeiro ou falso.
a) ( ) No caso de uma onda se propagando em uma corda na direção do eixo , cada ponto da corda conserva seu deslocamento .
b) ( ) Quando uma onda se propaga ao longo de uma corda esticada, cada elemento da corda possui a energia mecânica total constante.
c) ( ) Quando duas ondas senoidais iguais se propagam em sentidos opostos, o resultado é uma interferência totalmente destrutiva.
d) ( ) A amplitude de uma onda estacionária varia com a posição .
e) ( ) A velocidade transversal de um elemento de corda oscilando transversalmente em MHS é máxima quando está passando pela posição .
Passo 1
Fala galerinha, beleza? Bora brincar um pouco com essa questão sobre ondas em cordas!
Nesse problema, temos que marcar verdadeiro ou falso nas afirmativas sobre ondas em cordas. Vamos olhar primeiro para a afirmativa (a): “No caso de uma onda se propagando em uma corda na direção do eixo , cada ponto da corda conserva seu deslocamento .”
Essa afirmativa é claramente FALSA. Para uma onda transversal que se propaga na direção , o deslocamento transversal é uma função tanto da posição da corda como do tempo :
Fixando um ponto específico da corda, como por exemplo , temos que a posição desse ponto passa a ser uma função do tempo:
Observe que essa função varia com o tempo, de modo que o deslocamento de uma posição da corda não é conservado, ele varia com o tempo!
Passo 2
Agora vamos para a afirmativa (b): “Quando uma onda se propaga ao longo de uma corda esticada, cada elemento da corda possui a energia mecânica total constante.”
Para entender um pouco sobre isso, você precisa lembrar da fórmula da densidade de energia por unidade de comprimento transportada por uma onda em corda. A densidade de energia mecânica é
Nessa expressão, é a densidade de massa por unidade de comprimento da corda. A demonstração dessa expressão é um pouco complicada e muitas vezes não é feita nos cursos de física 2. Deixa eu responder o item (b) que eu depois eu faço algumas considerações extras sobre essa fórmula...
Como é uma função de , é fácil perceber que vai ser uma função tanto de como de . Isso mostra que pontos diferentes da corda podem ter energia diferentes. Desta forma, a afirmativa (b) também é FALSA!
Se você já estiver convencido com isso, pode pular para o passo 3. Agora vou brincar um pouco com essa densidade de energia!
Para uma onda harmônica,
Logo,
Daí, podemos tomar a média em um período, obtendo a densidade de energia média:
Como em um período, achamos
Observe que a densidade de energia média não depende da posição, isto é, ela se distribui uniformemente pela corda.
Agora olha que legal, podemos escrever
Mas , de modo que
Essa é a expressão da potência média que você deve conhecer 😉.
Passo 3
Vamos para a afirmativa (c) agora: “Quando duas ondas senoidais iguais se propagam em sentidos opostos, o resultado é uma interferência totalmente destrutiva.”
Quando a gente faz duas ondas senoidais idênticas que se propagam em sentidos contrários interferirem, nós não ganhamos uma interferência totalmente destrutiva, nós obtemos um padrão de onda estacionária:
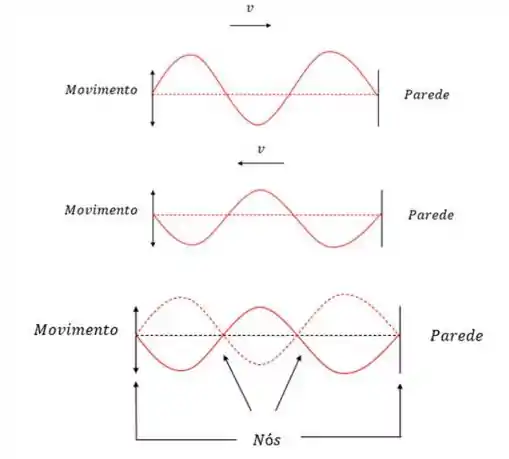
Portanto, a afirmativa (c) é FALSA!
Passo 4
A afirmativa (d) diz que “A amplitude de uma onda estacionária varia com a posição .” Vale lembrar que a equação do deslocamento de uma onda estacionária é
Muitas vezes chamamos de amplitude na posição . É fácil perceber que essa amplitude varia com . Desta forma, a afirmativa (d) é VERDADEIRA!
Uma outra forma de olhar para essa situação é pensar que alguns pontos da onda estacionária estão sempre parados com (os nós), enquanto outros oscilam, de modo que é evidente que a amplitude depende da posição!
Passo 5
Vamos terminar com a afirmativa (e): “A velocidade transversal de um elemento de corda oscilando transversalmente em MHS é máxima quando está passando pela posição .”
Aqui vale a mesma ideia de um sistema massa-mola: a velocidade é máxima quando a deformação é nula. Desta forma, a afirmativa (e) é VERDADEIRA!
Resposta
(a) F (b) F (c) F (d) V (e) V