. Um corpo está pendurado em equilíbrio em uma corda com um comprimento total e uma densidade de massa linear de . A corda passa em torno de duas polias leves sem atrito que são separadas por uma distância (Veja a figura abaixo). Suponha que a tensão na corda é de . Em que frequência deve vibrar a corda entre as polias a fim de formar o padrão de onda estacionária mostrado na figura ?
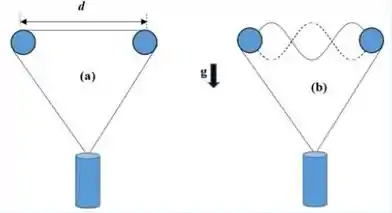
.
.
.
.
.
Passo 1
Vem comigo que a gente resolve essa questão juntos!
Temos aqui um caso onda estacionária em uma corda, a frequência da onda para essas situações é dada por:
Onde é referente ao harmônico de vibração, a velocidade da onda na corda e o comprimento total da corda que está vibrando.
O valor de já é dado no enunciado, é . Para acharmos ver podemos usar a seguinte equação que relaciona velocidade com a tensão aplicada na corda e sua massa linear.
Então fica tranquilo de achar essa velocidade já que o enunciado nos fornece o valor de e .
Agora para saber qual o harmônico de vibração temos que olhar a figura do enunciado, repare que a linha contínua tem máximos (não imposta se é para cima ou para baixo), então ela está vibrando no terceiro harmônico de vibração, logo .
Vamos atrás da frequência então!
Passo 2
Primeiro vamos achar a velocidade de propagação da onda na corda, temos:
Então temos que:
Passo 3
Então agora só falta encontrar a frequência de vibração, temos:
Logo temos que:
Olhando as alternativas no enunciado vemos que a que mais se aproxima é a letra .