Considere a onda . A superposição com qual das ondas a seguir produz uma onda estacionária?
Passo 1
Boom galera, pra descobrir isso, é mais fácil a gente analisar o que acontece com um pulso quando ele atinge uma extremidade fixa.
Passo 2
Quando um pulso atinge a extremidade fixa, o sentido de sua velocidade muda, e ele fica invertido:
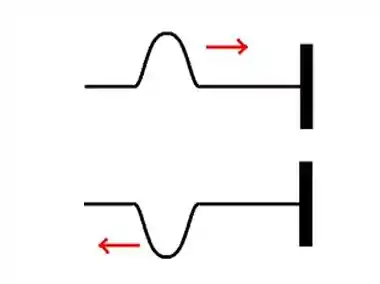
Então, vamos primeiro pensar na velocidade. Como ela muda de direção, o sinal que fica na frente da velocidade angular, , muda. Dai a gente precisa lembrar da regrinha:
Bom, como o sinal que tava na frente de era , ele passa a ser
Passo 3
Falta agora computar a inversão do pulso. Como você pode ver na figurinha, o pulso passa a ficar inclinado pra baixo. Então, as ordenadas do pulso passam a ser negativas.
Isso deve ser computado na equação colocando-se um na frente:
Assim, a onda escrita acima vai gerar pulsos invertidos que serão somados com a outra onda. Isso vai gerar nós e ventres, então a soma das ondas será chamada de onda estacionaria.
Resposta
a)