Uma corda de violino de de comprimento, com massa específica linear de , é colocada perto de um alto-falante alimentado por um oscilador de áudio de frequência variável. Quando a frequência do oscilador varia no intervalo de a , observa-se que a corda entra em oscilação apenas nas frequências de e .
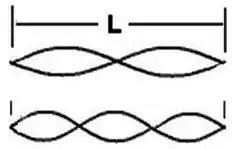
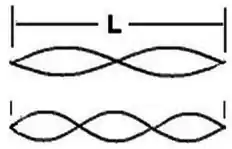
- Desenhe o padrão de onda estacionária na corda nos dois casos.
- Determine a tração na corda.
Passo 1
Temos que nas frequências e dois harmônicos. Em um dado harmônico temos meio comprimentos de onda na corda de comprimento
Por outro lado, temos a equação da onda
De forma que
Como a frequência evolui continuamente, as frequências que achamos para os harmônicos correspondem a harmônicos seguidos, ou seja
Dividindo as duas equações temos
O modo normal com frequência corresponde ao segundo harmônico e o modo com frequência corresponde ao terceiro harmônico. Agora é só desenhar esses modos!
Passo 2
Para determinar a tração podemos usar a seguinte equação
Já temos a densidade linear da corda, só falta a velocidade. Para isso basta olhar para o segundo harmônico (podia ser o terceiro também)
Passo 3
Agora falta só calcular a tensão
Não esquecendo de fazer a conversão
Resposta
(a)
(b)