Um grupo de pesquisa marinha está desenvolvendo boias com sensores de movimento para monitoração remota de ondas em alto-mar. De forma a testar o equipamento, três dessas boias são posicionadas ao longo de um rio num trecho sem curvas, na proximidade de uma barragem. A boia 1 estava posicionada junto à parede da barragem, a boia 2 está a 16 metros e a boia 3 a 36 metros .Considera as ondas na superfície da água como transversais.

x = 0 , e a onda na direção negativa de .

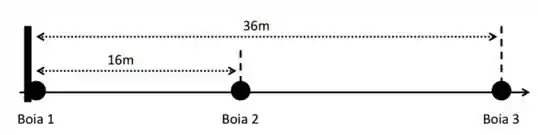
1. Se o sensor da boia 2 registrou o movimento após o sensor da boia , qual a velocidade da onda?
2. Os sensores registram um movimento oscilatório de período e amplitude .Qual o comprimento de onda e a frequência desta onda.
3. Diferentemente dos sensores das boias 2 e 3, o sensor da boia 1 registra que a amplitude de oscilação é de . Escreva a equação da onda incidente, da onda refletida pela barragem, e da onda total resultante ( para definir a fase inicial, assuma que é um ponto de máximo.
4. Considerando a interferência entre a onda incidente e a onda refletida, qual será a amplitude de oscilação registrada pelos sensores das boias 2 e 3 após a reflexão?

b):

Bom, a frequência é o posto do período, logo:

Pra acha o comprimento de onda, basta a gente aplicar a fórmula:

c):

As ondas vão ter o formato:

O item nos diz que a onda registrada tem amplitude , ou seja, o dobro da amplitude .Além disso, o período dessas ondas é Com esse período, podemos calcular o e o

Logo:

E a amplitude é igual a Logo, a equação da onda incidente, considerando-se que ela está se movendo no sentido negativo do eixo

Como não há perdas de energia nem interferências, a equação da onda refletida pela parede será similar a essa, apenas com o sinal que acompanha a velocidade angular invertido (pra indicar a mudança de sentido da esquerda pra direita):

Observe que nas equações as fases inicias são iguais a zero. Isso ocorre para que em haja um ponto de máximo. Por quê? Por que se isso acontece:

Se é um máximo:

Enfim, vamos calcular agora a equação da onda resultante. Observe isso: como a onda que é refletida pela parede tem a mesma defasagem, a mesma velocidade angular e o mesmo número de onda da onda incidente, de que tipo de onda será a onda resultante?

Será uma onda estacionária!:o

Ok! Então não vai ficar fazendo contas, certo? Vamos seguir o modelo de uma onda estacionária:

Logo:

d):

Vamos considerar a nossa origem na extremidade esquerda do sistema. As posições das boias 2 e 3 são, então, respectivamente, e Na boia 2:

Logo, como a amplitude da oscilação ali é , ou seja, é máxima, na boia 2 existe um ventre.

E em

Como :

Logo, na boia 3 há um nó!