Uma corda de nylon de uma guitarra tem uma densidade linear de e está sob tensão . Os suportes fixos distam . A corda vibra no trem de onda estacionário visto na figura a seguir.
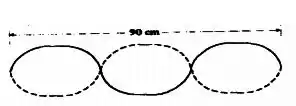
Calcule:
A velocidade
O comprimento de onda
A frequência das ondas componentes cuja superposição causa esta vibração
Passo 1
Primeiro vamos resolver a :
Encontrar a velocidade é simples nesse caso, pois temos a Tensão da corda e a sua densidade linear. A gente deve usar essa equação, então:
Sendo:
Temos:
Pronto! Vamos usar essa informação também na .
Passo 2
Como a onda é estacionária, a gente pode usar a relação:
Onde é comprimento total do fio. Isolando :
Como são 3 picos, ou 3 metades de onda, Além disso, o enunciado nos diz que . Substituindo:
Passo 3
c)
Nas letras anteriores a gente conseguiu achar o ! Agora, queremos a frequência, por isso vamos utilizar esse valor na equação:
Aplicando o valor de e :
Resposta
Resposta: