UFF – Física III – P2 – 2022.1 – Q10
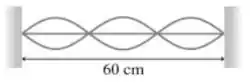
Uma onda estacionária numa corda está oscilando com frequência de 500 Hz, como mostra a figura. A densidade linear de massa da corda é 10,0g/m. Qual é a tensão na corda?
Passo 1
E aí, galerinha! Tudo na paz por aí?
O primeiro passo é pegarmos as informações do nosso problema. O enunciado nos deu a frequência e a densidade de massa da corda, ou seja:
Uma equação que pode nos fornecer o comprimento de uma corda e relacionar o número de harmônicos é:
Onde é o número de harmônicos (basicamente são quantos pares de subida e descida nós temos, nesse caso são 3) e L é o comprimento da corda.
Tá, e qual equação vai me dar a tensão da corda?
Opa, mas percebeu que eu consigo substituir pela equação de ... hummmmmmmmm então pensa aí rapidinho e me fala qual seriam os próximos passos!
Pensou?
Agora vem conferir comigo se você pensou direitinho!
Passo 2
Primeiro, vamos isolar da equação de :
Agora vamos substituir na equação da tensão:
Opa, que maravilha, agora nessa tensão está em função apenas de variáveis que conhecemos os valores.
UHUUUUULLLLL, FECHAMOS A QUESTÃO!!!