Interferência
Uma corda de violão com densidade linear de , presa em ambas as extremidades, está sujeita a uma tensão de .
- Com que velocidade se propaga um pulso transversal nessa corda?
- Para um dado comprimento fixo, desenhe os três primeiros harmônicos. Para os diversos modos de vibração, escreva a relação entre e os respectivos comprimentos de onda .
- Qual deve ser o comprimento da corda para que sua frequência fundamental seja ?
- Para tocar uma nota de frequência , prende-se a corda com um dedo, de forma a utilizar apenas uma fração do seu comprimento. Qual é essa fração ?
Passo 1
a):
Vamos usar aqui a expressão de Taylor:
Aqui a gente só precisa ter o cuidado de usar as unidades do SI. Então é preciso converter a unidade de massa da densidade linear:
Então:
Passo 2
b):
A relação entre o comprimento de onda de um determinado harmônico e o comprimento do fio é dada por:
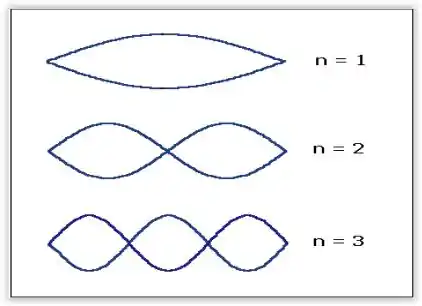
Passo 3
c):
Sendo a frequência de uma corda dada por:
A frequência fundamental é o pra Isso é:
Esse valor deve ser igual à Logo:
Passo 4
d):
Essa parte da questão nos quer dizer que para um determinado comprimento , que é uma fração de , a frequência do harmônico fundamental é . Isso é:
E . Queremos achar . Assim:
Resposta
a):
b):
c):
d):
Exercícios de Livros Relacionados
Na figura, uma corda presa a um oscilador senoidal no ponto P e apoiada em um suport no ponto Q é tensionada por um bloco de massa m . A distância entre P e Q é L = 1,20 m e a freqüência do oscilador
Na figura, uma corda, presa a um oscilador senoidal no ponto P e apoiada em um suporte no ponto Q , é tensionada por um bloco de massa m . A distância entre P e Q é L=1,20m , a massa específica linear
A equação de uma onda transversal que se propaga em uma corda é y = 0,15 s e n ( 0,79 x - 13 t ) onde xey estão em metros e t está em segundos. (a) Qual é o deslocamento y em x=2,3m e t=0,16s ? Uma se
Utna corda d e120c m de comprimento está esticada entre dois suportes fixos. Qual é (a) o maior, (b) o segundo maior e (c) o terceiro mnaior comprimento de onda das ondas que se propagam na corda para
Uma onda estacionária em uma corda é descrita por y x , t = 0,40 s e n 5 π x cos 40 π t Onde xey estão em metros, e t em segundos. Para x ≥ 0 qual é a localização do nó com (a)o menor (b) o segundo