Uma corda oscila no terceiro harmônico, de acordo com a equação . Quais são, respectivamente, o comprimento da corda e a velocidade transversal de uma partícula da corda no ponto para ?

Como vocês já devem ter pensado um pouquinho, bora para nossa resolução. Temos que a equação de ondas estacionárias para o eixo é do seguinte formato: . Assim, comparando essa equação genérica com a que nos foi fornecida nessa questão descobrimos que :

Lembrando que representa o número de onda, ou seja, quantos comprimentos de onda possuem em um ciclo de . Dessa forma:

Portanto poderemos afirmar que é:

Entretanto não queremos apenas o comprimento de onda, na verdade queremos saber qual é o tamanho da corda utilizada.

Recapitulando, no passo anterior descobrimos qual é o valor do comprimento de onda e não o tamanho da corda, mas a questão nos deu uma dica. O enunciado diz que a equação se refere a uma onda estacionária que oscila no terceiro harmônico. Assim como a figura a seguir:

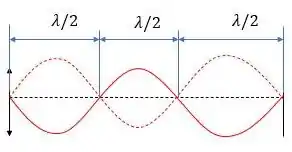
Uma onda que oscila no terceiro harmônico significa comprimento da corda é igual três vezes meio comprimento de onda, ou seja,

Onde representa o tamanho da corda.

Como já encontramos o valor do comprimento de onda que é , basta substituirmos na equação acima.

Agora crianças, precisamos encontrar qual é a velocidade transversal de uma partícula da corda em e . Como é desejável encontrar a velocidade em um ponto específico da corda é ideal derivarmos a expressão de comprimento para em seguida substituirmos com os valores dados. Bora botar a mão na massaaaa!

Sendo e :

E aí? Essa resolução te ajudou?? Responde Aí!

Beijinhos e bons estudos :)