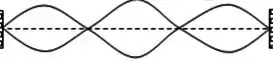
Numa experiência de laboratório, ondas de 120 Hz são excitadas numa corda com densidade linear igual a 0,5 g/m conforme a figura. O copo preso na extremidade da corda tem massa igual a 50 g e contém, inicialmente, 250 g de água.
Observa-se que o copo está furado e que a água vai escoando lentamente. Suponha que o comprimento da corda seja mantido fixo (L = 0,5 m)
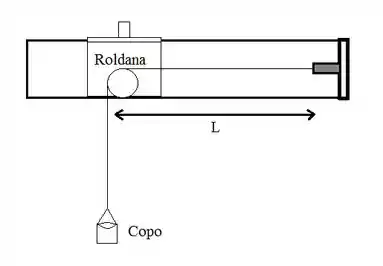
a) Calcule as massas de água no copo para as quais serão observadas ressonância na corda.
b) Desenhe a onda estacionária na corda para a primeira ressonância a ser observada.
Passo 1
a) As frequências de ressonância são:
Mas a frequência no caso é dada, constante e igual a 120 Hz.
Quem vai variar aqui no caso, então, vai ser a velocidade!
Vamos isolar a velocidade:
Trocando os valores de L e f:
Show!
Passo 2
Tem uma outra fórmula pra velocidade. É:
Em que:
Não esqueça de transformar as unidades!!!
Por equilíbrio de forças no copo, a tração na corda vai ser igual ao peso do copo com água. Então:
Vamos substituir então:
Passo 3
Vamos igualar agora as duas fórmulas que encontramos pra velocidade:
Elevando ao quadrado dos dois lados:
Como n é o número do harmônico, vai ser um número inteiro. Vamos fazer uma tabelinha pra massa de água em função de n:
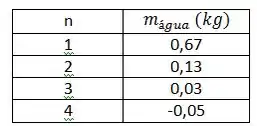
Pra é impossível ter ressonância, porque a massa de água vai ser sempre menor ou igual a 0,25 kg. Pra , a massa de água tem valor negativo. O que é impossível.

Então será observada ressonância na corda para as massas de água:
Passo 4
b) Vamos lembrar que:
Se :
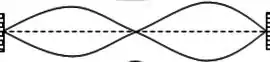
Se :
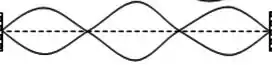
Resposta
a) e
b):
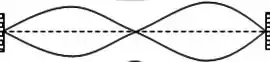
: