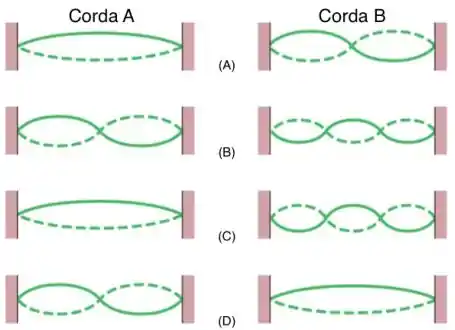
Duas cordas A e B (ver figura) possuem o mesmo comprimento e a mesma densidade linear, mas a corda A está submetida a uma tensão menor que a corda B. A Figura mostra quatro situações, de (A) a (D), nas quais existem ondas estacionárias nas duas cordas. Em que situação existe a possibilidade de que as cordas A e B estejam oscilando com a mesma freqüência natural?
(a) Situação B.
(b) Situação D.
(c) Situação A.
(d) Em nenhuma das situações.
(e) Situação C.
Passo 1
Uma onda na corda tem velocidade
Onde T é a tensão e a densidade linear da corda.
As ondas estacionárias que se formam numa corda com ambas as extremidades fixas possuem frequências:
Onde é a velocidade, L é o comprimento e Substituindo a velocidade:
Passo 2
Queremos uma situação em que as duas ondas tenham a mesma frequência:
Cortando os termos iguais e rearranjando:
Como , então , logo
Para as frequência serem iguais A tem que estar num harmônico maior do que B.
A única situação em que isso ocorre é a situação D, pois .
Resposta
(b) Situação D.