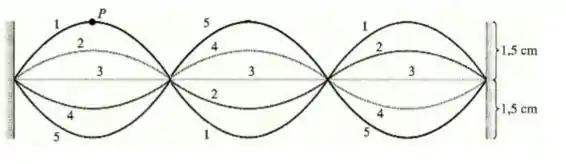
​ Uma corda de de comprimento está vibrando sob uma tensão de . Os resultados de cinco fotografias estroboscópicas sucessivas são mostrados na figura abaixo. A taxa do estroboscópico é fixada em 5000 flashes por minuto, e observações revelam que o deslocamento máximo ocorreu, em relação à posição de equilíbrio da corda, nos flashes 1 e 5, sem nenhum outro máximo no intervalo entre eles. Qual a massa da corda?

Já vimos que a velocidade de uma onda é dada por

Opa, não temos nenhum dos dois! Keep Calm!

Conseguimos achar o comprimento de onda e a frequência através da foto e dos dados que o enunciado nos forneceu.

Primeiro vamos descobrir o comprimento de onda. Sendo uma onda estacionária, vimos que conseguimos relacionar o comprimento de onda com o número do harmônico .

Pela imagem, vemos que , assim o comprimento de onda é

Agora, só falta descobrirmos a frequência, para termos tudo para descobrirmos a massa da corda.

O problema não falou nada sobre frequência, mas falou sobre tempo, o que nos faz pensar em período.

Ele disse que o deslocamento máximo ocorreu entre a foto e , 0 que que dizer que essas fotos são nodos, assim conseguimos descobrir o tempo que se passa entre dois nodos.

Onde é o número de fotos batidas e é o intervalo de tempo entre cada foto.

Bem, depois da foto , foram batidas 4 fotos até termos a foto e, então

Show, e melhor ainda, pois o enunciado nos fala que as fotos têm um intervalo de fotos por minuto.

Então o intervalo entre fotos é de

Como queremos esse intervalo em segundos, temos

Assim o tempo de um nodo até o outro é

Porém entre dois nodos temos apenas metade do comprimento da onda, então o período da onda é

Como a frequência é o inverso do período

Agora já podemos calcular a massa da corda

Como a velocidade é

Então

Substituindo pelos valores que já temos