UFRJ – Física 2 2019.2 – Segunda Chamada – Questão 2
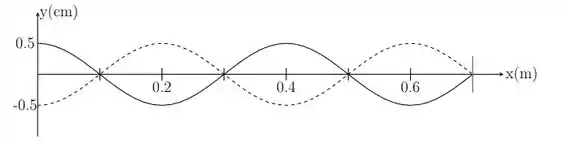
Uma corda fixa em um dos extremos e livres para oscilar no outro, vibra num dado modo normal. A velocidade de propagação das ondas nesta corda vale . A figura mostra o perfil da corda num dado instante em que todos os deslocamentos são máximos.
- Determine o comprimento de onda e a frequência de oscilação da corda neste modo normal.
- Determine o comprimento de onda e a frequência de oscilação para o modo normal de maior frequência logo abaixo deste.
- Determine as posições dos nós no modo do item .
- Escreva a equação da onda estacionária que descreve a oscilação da corda para este novo modo normal. (Suponha a mesma amplitude do modo dado no enunciado e que os deslocamentos são máximos em ).
Passo 1
Fala galera, tudo bem? Vou ajudar você a resolver essa questão! Vamos lá?
Letra (a):
Sabemos que a distância entre dois nós equivale a metade de um comprimento de onda inteiro. E pelo gráfico temos que a escala vale . Sendo assim, metade de um comprimento vale , logo um inteiro é o dobro disso:
E como temos a velocidade, podemos calcular a frequência:
Passo 2
Letra (b):
Quando temos uma extremidade fixa e uma livre, os modos normais são dados em múltiplos impares de . No gráfico temos quartos de comprimentos de onda, olha só:
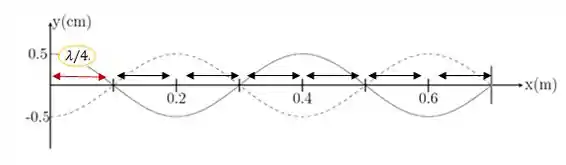
Então modo natural abaixo dele é quartos de comprimento de onda:
E agora com o novo comprimento de onda podemos calcular a frequência associada a esse modo:
Passo 3
Letra (c):
Como o extremo esquerdo em é o livre, o primeiro nó vai acontecer depois de , ou seja:
A partir daí, ele se repete a cada . Ou seja, a cada . Então o próximo nó vai ser:
Passo 4
Letra (d):
A equação para uma onda é:
A amplitude é dada em e vale . O número de onda é dado em função do comprimento de onda:
A velocidade angular é:
Assim podemos montar a equação dessa onda:
Beleza?
Pronto pra próxima questão? =)