Duas cordas e possuem o mesmo comprimento e a mesma densidade linear, mas a corda está submetida a uma tensão maior que acorda . A figura abaixo mostra quatro situações, de a , nas quais existem ondas estacionárias nas duas cordas.
Em que situação existe a possibilidade de que as cordas e estejam oscilando com a mesma frequência natural?
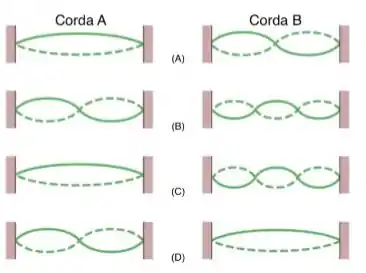
Situação .
Situação .
Situação .
Situação .
Em nenhuma das situações existe a possibilidade de que as cordas e oscilem com a mesma freqüência natural.
Passo 1
A frequência natural em uma onda estacionaria é dada por:
Onde é o número de antinós, a velocidade e o comprimento da corda
Como a tensão nas cordas são diferentes então a velocidade da onda na corda irá ser diferente, porque a velocidade é dada por:
Onde é a tensão aplicada na corda e é densidade linear na corda.
Então podemos escrever a equação da frequência natural em função da tensão e da densidade linear
Assim, podemos achar a equação da frequência natural para cada corda.
E
Passo 2
Como queremos a figura em que a frequência natural seja a mesma, então vamos igualar as frequências
Como o enunciado nos disse o comprimento e densidade linear são as mesmas em ambas as cordas. Podemos cortar esses temos da igualdade
Dado que é maior que , então para a igualdade ser satisfeita deve ser maior que
E a única figura que isso acontece é a última, em todas as outras figuras é maior que
Resposta
Alternativa