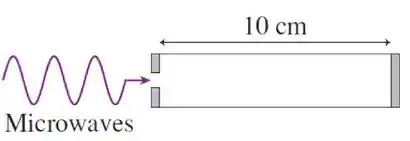
Microondas são enviadas, através de um pequeno orifício, para o interior de uma "cavidade ressonante", a qual consiste de um cilindro de de comprimento com extremidades refletivas (fig). A fonte de microondas pode emitir ondas em
toda a faixa de frequências indo de a . Queremos usar esta fonte para gerar ondas estacionárias com um nó no centro da cavidade. Sendo o índice que enumera os modos normais, isto será possível
A) para todos os valores ímpares de
B) para todos os valores pares de
C) para certos valores pares de
D) para certos valores ímpares de
E) para nenhum valor de
Passo 1
Para que haja uma onda estacionária no interior do cilindro que haja meio comprimentos de onda no comprimento do cilindro, ou seja
Os padrões para as ondas estacionárias indo do primeiro ao quarto harmônico é mostrado na figura abaixo
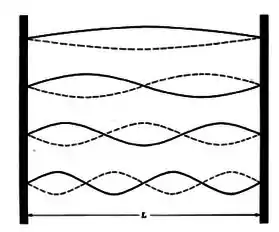
Para que tenhamos um nó no centro do cilindro é necessário que seja par!
Passo 2
Temos que uma onda tem que obedecer
Como a frequência varia de a temos que só temos alguns valores possíveis para o comprimento de onda e consequentemente só alguns possíveis valores pares de .
Resposta
(C)