O movimento de uma partícula, descrito pela função , é mostrado no gráfico abaixo.
Dele deduzimos que:
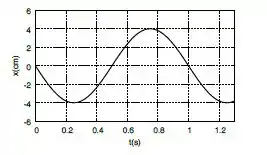
- e
Passo 1
Bom, essa questão é bem maneira e podemos soluciona-la basicamente analisando o gráfico. A amplitude do gráfico é dada pela diferença entre a origem e o ponto de crista, parâmetro que podemos ver pelo encontro da linha azul mostrada no gráfico abaixo:
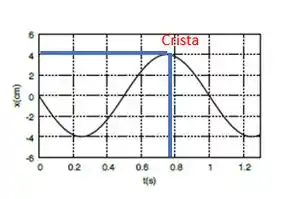
Como nos mostra a figura, a amplitude da onda é 4cm! Até que essa parte foi de boas, né!? =)
Passo 2
Podemos fazer o seguinte:
Quando :
Agora precisamos saber se é + ou -!
Passo 3
Pelo gráfico, a gente consegue ver que o período é igual a 1. Então:
Daí tiramos que:
Beleza, então nossa função é:
Vou substituir agora o valor :
Mas pelo gráfico, vemos que em T/4 a posição é -4 cm. Então:
Ficamos então com letra B.
Resposta
Letra B
Exercícios de Livros Relacionados
Na figura, uma corda presa a um oscilador senoidal no ponto P e apoiada em um suport no ponto Q é tensionada por um bloco de massa m . A distância entre P e Q é L = 1,20 m e a freqüência do oscilador
Na figura, uma corda, presa a um oscilador senoidal no ponto P e apoiada em um suporte no ponto Q , é tensionada por um bloco de massa m . A distância entre P e Q é L=1,20m , a massa específica linear
A equação de uma onda transversal que se propaga em uma corda é y = 0,15 s e n ( 0,79 x - 13 t ) onde xey estão em metros e t está em segundos. (a) Qual é o deslocamento y em x=2,3m e t=0,16s ? Uma se
Utna corda d e120c m de comprimento está esticada entre dois suportes fixos. Qual é (a) o maior, (b) o segundo maior e (c) o terceiro mnaior comprimento de onda das ondas que se propagam na corda para
Uma onda estacionária em uma corda é descrita por y x , t = 0,40 s e n 5 π x cos 40 π t Onde xey estão em metros, e t em segundos. Para x ≥ 0 qual é a localização do nó com (a)o menor (b) o segundo