PUC-RIO- FIS 2 1041– G2 2019.2
Uma corda de violino com de comprimento oscila no modo e a velocidade da onda na corda é . Determine o comprimento de onda da onda sonora produzida.
Passo 1
Muita atenção no enunciado!! Ele quer o comprimento da onda sonora produzida pelo violino. Acompanha aqui comigo que vai ser moleza encontrar esse valor.
Passo 2
Um violino tem ambas as extremidades da corda fixas. E se ele está no modo de vibração , temos que, dois modos de vibração são formados entre os pontos que fixam as cordas do violino. Mas o enunciado no fala o comprimento da corda, que mede .
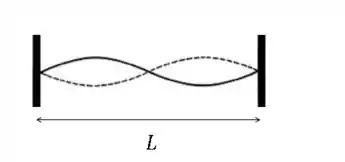
Mas vejam só, temos exatamente 1 comprimento de onda entre os pontos de fixação.
Mas é isso? Essa é a resposta? Não! Esse é o comprimento da onda na corda. Essa corda vibra nesse harmônico, com uma velocidade de propagação, na corda, produzindo uma frequência. Que viaja pelo ar e então chega aos nossos ouvidos.
A frequência que está relacionada a esse comprimento de onda na corda é:
Agora, essa frequência viaja no ar (então a velocidade de propagação é a velocidade do som no ar, ), até nossos ouvidos. O comprimento de onda que ouvimos é
Esse sim é o comprimento da onda sonora que é produzida pelo violino.