PUC - RIO- FIS 2 1041– G2 2019.2
A corda de um violino (as duas bordas são fixas) foi afinada de modo que seu primeiro modo normal seja uma onda estacionária de frequência de . A corda possui massa específica linear de e está sujeita a uma tração de . A figura serve como guia.
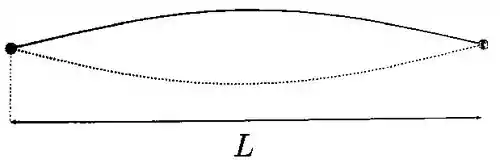
a) Quanto vale o tamanho da corda?
Para que a mesma corda vibre em outra frequência , o violinista a prende com seu dedo em um ponto para que ela vibre em apenas uma fração de tamanho da corda (ver figura) .
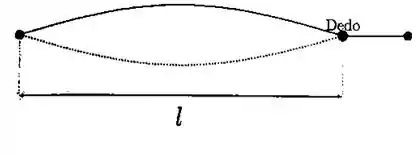
(b) Calcule a razão
Passo 1
a)
O enunciado fala que aquele é o primeiro modo de vibração, . A frequência do n-ésimo modo normal de vibração é
O é modo de vibração, como esse é o primeiro, . A frequência é a frequência do n-ésimo modo, no nosso caso, já foi dado no enunciado. é o que queremos saber.
E é a velocidade de propagação da corda, que é dada por:
Substituindo:
Pelos dados do enunciado:
Note que o passamos para unidades do SI.
Uhull! Tranquilo?
Passo 2
b)
Mesmo com o dedo, ainda temos só um modo de vibração, então . A frequência . Então:
A velocidade da corda, como vimos, é
Como nem o e nem muda quando coloca-se o dedo, a velocidade permanece a mesma que era antes.
Então
Fazendo a razão:
Resposta
a)
b)