A taxa de transferência de energia por uma onda ao longo de uma corda (a potência instantânea) é dada por:
Onde é a tensão.
- Usando a expressão (1), obtenha para uma onda estacionária dada por:
- Calcule a potência média por período transportada pela onda para todo o
- Para uma onda estacionária dada pela expressão (2), faça gráficos de e do deslocamento em função de para: , , , e .
- Qual o valor da potência instantânea nos nós e nos ventres da onda?
Passo 1
a)
Bom, aqui a gente só precisa calcular as duas derivadas parciais da fórmula e fazer o produto entre elas. é a tensão da corda, então vamos considerá-la como um dado do problema. Assim:
Derivando a expressão em relação ao tempo:
E em relação a :
Logo:
Bom, o produto vai dar positivo. Arrumando isso:
Usando a expressão:
Vamos usar isso pra e
Passo 2
b)
O valor médio tem uma dependência temporal, certo? Então, olhando pra expressão da potência, nós podemos concluir que a potência média vai depender do termo da expressão que depende do tempo, ou seja,
E qual o valor médio disso?
Bem, é uma função senoidal, logo tem valor em um período como o valor médio. (Lembra, o seno varia de a 1, entre eles fica o ).
Logo, a potência média será:
Passo 3
c)
Pra :
E:
Logo o gráfico normalizado será:
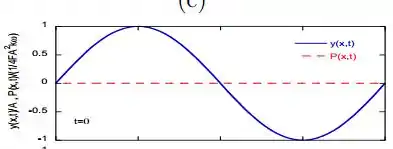
Onde a linha contínua representa e pontilhada a potência.
Para :
E a potência:
Logo:
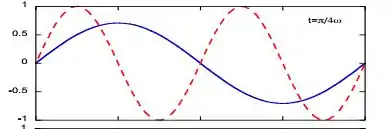
Para
E a potência:
Logo:
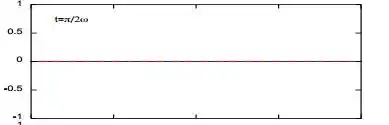
Pra
Logo:
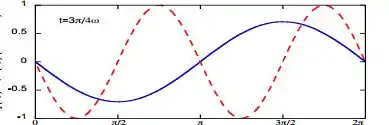
Passo 4
d)
As ondas estacionárias possuem nós e ventres distanciados de si por uma distância .
Então podemos dizer que os pontos onde estão os nós e ventres de uma onda estacionária numa corda são:
Só que olhando a expressão da potência numa corda:
Percebemos que a potência será nula quando:
Opa! Esses são os nós e ventres. Ou seja, nos nós e ventres a potência é igual a :
Resposta
a)
b)
c)
Gráficos acima.
d)