Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Ondas Estacionárias

Ver Teoria
Exercício 911234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889909293949596979899

Enunciado

Física 3 - UFF; P2 de 2019.2

10 - Uma onda transversal tem suas oscilações no eixo y   e se propaga ao longo do eixo x . A diferença entre um ponto de mínimo e um de máximo da onda no eixo y   é de 1,0   m e no eixo x   é de 2,0   m . Suponha que as condições iniciais da mesma resulte em uma constante de fase igual a zero e que a fonte gere as oscilações propagantes em uma taxa de 2   repetições por segundo. Qual a função que melhor descreve esta onda? (Considere x em metros e t   em segundos)

  1. y ( x ,   t )   =   ( 0,5   m )   s e n   [ ( π )   x   -   ( 4 π )   t ]
  2. y ( x ,   t )   =   ( 1,0   m )   s e n   [ ( π / 2 )   x   -   ( 4 π )   t ]
  3. y ( x ,   t )   =   ( 1,0   m )   s e n   [ ( π / 2 )   x   -   ( π )   t ]
  4. y ( x ,   t )   =   ( 1,0   m )   s e n   [ ( π )   x   -   ( 4 π )   t ]
  5. y ( x ,   t )   =   ( 0,5   m )   s e n   [ ( π / 2 )   x   -   ( 4 π )   t ]

Passo 1

Bem, a onda transversal é aquela típica que conhecemos. Como ela tem as oscilações no eixo y e se propaga em x ela é desse tipo aqui:

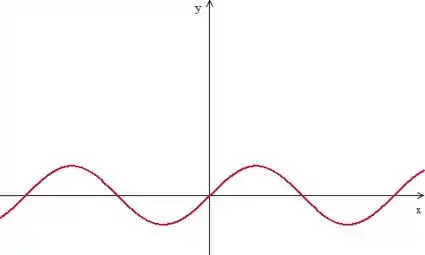
Veja que como no ponto x = 0 ela tem y = 0 , ela de fato tem uma constante de fase igual a zero!

Agora vamos construir a equação dela de acordo com as especificações.

Passo 2

A equação da onde no geral tem esse formato aqui:

D x ,   t = A sin ⁡ k x - ω t + ϕ 0

Onde ϕ 0 é a constante de fase que no nosso caso é 0 . D é o eixo onde ocorre as oscilações (eixo y ):

y x ,   t = A sin ⁡ k x - ω t

A é a amplitude da onda e basicamente é essa alturinha aqui:

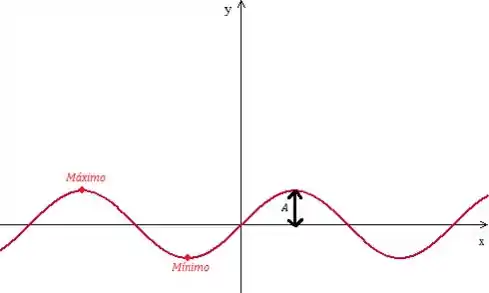
De acordo com o nosso problema, a diferença entre um ponto de mínimo e um de máximo é de 1 m . Logo, A vai ser a metade disso:

A = 0,5 m   →

y x ,   t = 0,5 m sin ⁡ k x - ω t

Quanto a k , ora...

k = 2 π λ

Onde λ é o comprimento de onda que basicamente se refere a esse tamanho aqui:

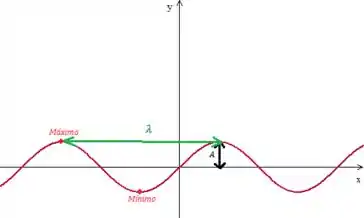
Como o problema também nos disse que a diferença entre um ponto de máximo e de mínimo no eixo x era de 2 m , λ será o dobro disso:

λ = 2 ⋅ 2 m = 4 m   →

y x ,   t = 0,5 m sin ⁡ 2 π x 4 - ω t   →

y x ,   t = 0,5 m sin ⁡ π x 2 - ω t

Só está faltando ω agora! Venha comigo

Passo 3

Ora, sabemos que ω é igual a:

ω = 2 π T

Onde 1 / T é igual a frequência f :

ω = 2 π f

f é o número de repetições por segundos, o que no caso é 2 . Então...

ω = 4 π

E concluímos que...

y x ,   t = 0,5 m sin ⁡ π x 2 - ω t   →

y x ,   t = 0,5 m sin ⁡ π x 2 - 4 π t   →

y ( x ,   t )   =   ( 0,5   m )   s e n   [ ( π / 2 )   x   -   ( 4 π )   t ]

Resposta

Letra E.

Exercícios de Livros Relacionados

Na figura, uma corda presa a um oscilador senoidal no ponto P e apoiada em um suport no ponto Q é tensionada por um bloco de massa m . A distância entre P e Q é L = 1,20 m e a freqüência do oscilador
Na figura, uma corda, presa a um oscilador senoidal no ponto P e apoiada em um suporte no ponto Q , é tensionada por um bloco de massa m . A distância entre P e Q é L=1,20m , a massa específica linear
A equação de uma onda transversal que se propaga em uma corda é y = 0,15 s e n ( 0,79 x - 13 t ) onde xey estão em metros e t está em segundos. (a) Qual é o deslocamento y em x=2,3m e t=0,16s ? Uma se
Utna corda d e120c m de comprimento está esticada entre dois suportes fixos. Qual é (a) o maior, (b) o segundo maior e (c) o terceiro mnaior comprimento de onda das ondas que se propagam na corda para
Uma onda estacionária em uma corda é descrita por y x , t = 0,40 s e n 5 π x cos ⁡ 40 π t Onde xey estão em metros, e t em segundos. Para x ≥ 0 qual é a localização do nó com (a)o menor (b) o segundo