A figura mostra um fio composto de dois pedaços emendados de fios de um material 1 e de um material 2 de mesma área de seção transversal com densidades volumétricas , no caso do material 1 e para o material 2. Sabe-se que o fio do material 1 tem de comprimento, que na extremidade do fio do material 2 está pendurado um bloco com de massa e que a distância entre a junção dos fios e a roldana de suporte é . Ao usar um gerador de ondas externo de frequência ajustável para criar ondas transversais no fio composto, determine (assuma que tanto a extremidade esquerda do fio ligada ao gerador quanto aquela em contato com a roldana são nós):
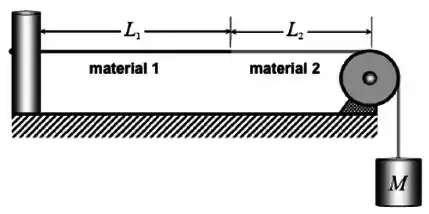
Dica: para simplificar suas contas, use como valor para a aceleração da gravidade .
(a) a velocidade de propagação v das ondas progressivas em cada pedaço do fio composto;
(b) a ordem dos harmônicos mais baixos que aparecem na corda quando a frequência f da fonte é ajustada de modo a originar uma onda estacionária com nó exatamente na junção dos fios;
(c) a frequência f do gerador externo correspondente à onda estacionária do ítem anterior.
(d) os comprimentos de onda e em cada fio na configuração do item (b).
Passo 1
a) A velocidade de uma onda que se propaga em uma corda é
Onde T é a tração, no caso , e é a densidade linear de massa da corda:
Como as cordas são cilíndricas, então
Então temos
Passo 2
b) Como na junção dos dois fio temos um nó, então é como se tivéssemos cordas independentes, ambas com as extremidades fixas.
Uma onda estacionária em uma corda vibrante tem frequência de ressonância:
Como o gerador de ondas vai excitar a mesma frequência nas duas cordas, temos que as frequências tem que ser iguais:
Então os menores valores que satisfazem as condições são e .
Passo 3
c) Uma onda estacionária é gerada justamente quando o sistema entra em ressonância: a frequência externa é igual a uma frequência natural do sistema:
Jogando os valores da corda 1 (daria o mesmo para a corda 2):
Passo 4
d) Estamos no 5º harmônico na corda 1 e no 2º harmônico na corda 2. Um esboço disso:
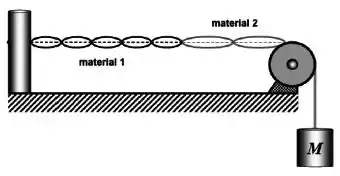
Na corda 1 temos 2,5 comprimentos de onda:
Na corda 2 temos 1 comprimento de onda:
Resposta
(a) ,
(b) ,
(c) 250 Hz
(d) ,