USP, Sem Campus, Física 1, Coletâneas de Exercícios - Parte II - Colisões, Torque, Cinemática Angular, Questão 33c
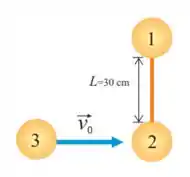
33. Um haltere formado por dois discos e iguais de massa unidos por uma barra rígida de massa desprezível e comprimento repousa sobre uma mesa de ar horizontal. Um terceiro disco de mesma massa , desloca-se com atrito desprezível e velocidade sobre a mesa, perpendicularmente ao haltere, e colide frontalmente com o disco , ficando colado a ele.
(c) Determine a velocidade angular do sistema depois da colisão.
Passo 1
Fala aí, querido!! Tudo certinho? Bora resolver esse probleminha? 😉
Nesse problema temos dois discos de massa presas por uma barra de massa desprezível e comprimento . Um terceiro disco viaja com velocidade em direção ao disco que ao colidirem, se grudam e o sistema inteiro começa a se mover.
Com isso queremos obter a velocidade angular do sistema após a colisão!
E aí, parece complicado? 👀
Para resolver esse problema, podemos aplicar o teorema da conservação do momento angular...
No caso, inicialmente, podemos calcular como o produto vetorial
Já após a colisão, podemos calcular como
Tudo certo? 😉
Passo 2
Vamos começar calculando o momento angular no instante antes da colisão...
O sistema com dos discos e estão parados, portanto não possuem momento angular... já o disco tem movimento e seu momento angular em relação ao centro de massa (centro de massa do sistema em ) e a velocidade ...
Vamos trabalhar em modulo que é mais fácil nesse caso...
Já no instante final (após a colisão), será dado por
Onde do sistema é dado pelo teorema dos eixos paralelos...
Igualando e
Isolando e simplificando o resultado, vamos obter
Como ...
Sacou como faz? Responde Aí! 😉
