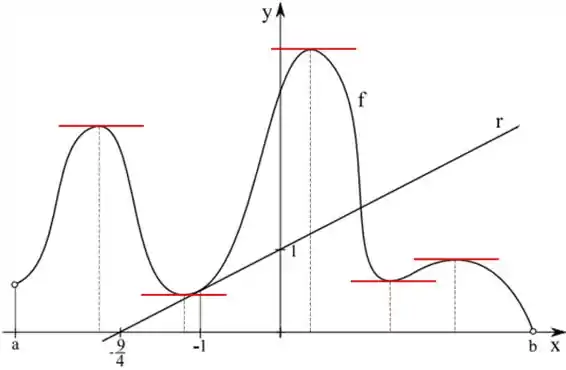
Considere a função definida pelo gráfico abaixo.
- Indique os pontos onde é zero. (Justifique graficamente, desenhando a reta tangente)
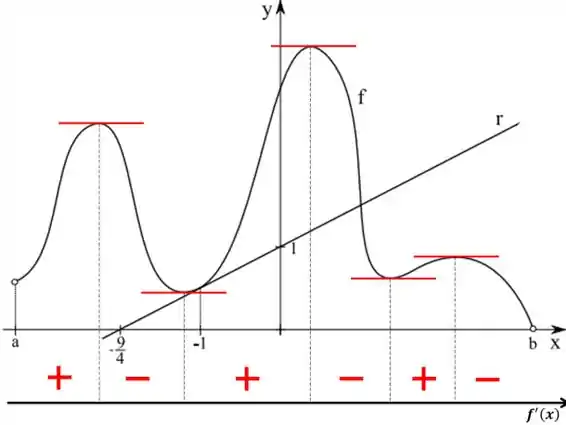
- Indique os intervalos onde é positiva. Indique os intervalos onde é negativa. (Justifique graficamente)
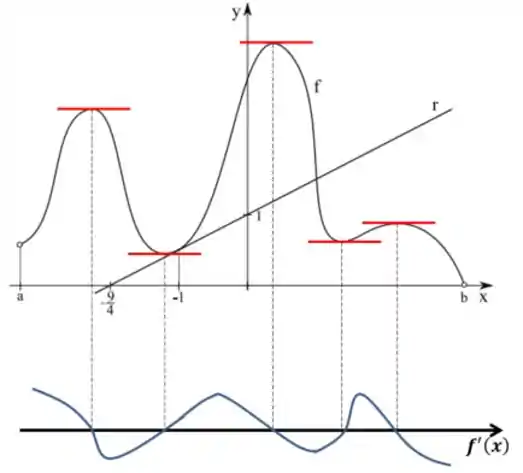
- Faça um esboço do gráfico da
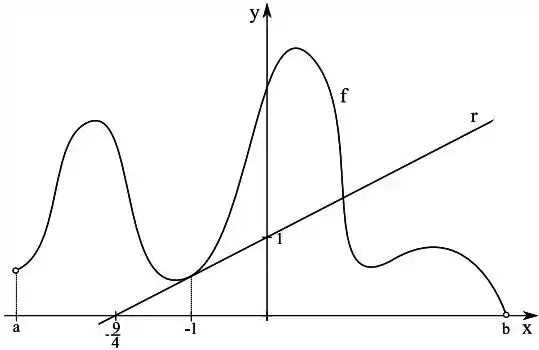
- Sabendo que a reta é tangente ao gráfico da em , calcule e
Passo 1
Ele quer os pontos onde a derivada é , mas quando isso acontece? Lembra que os pontos críticos são quando a derivada é ? Então nos máximos e mínimos dessa função vamos ter a derivada sendo .
Outro detalhe a se perceber é que quando a reta tangente for horizontal vamos ter a derivada sendo , vamos ver o gráfico disso, marcando cada um desses lugares.
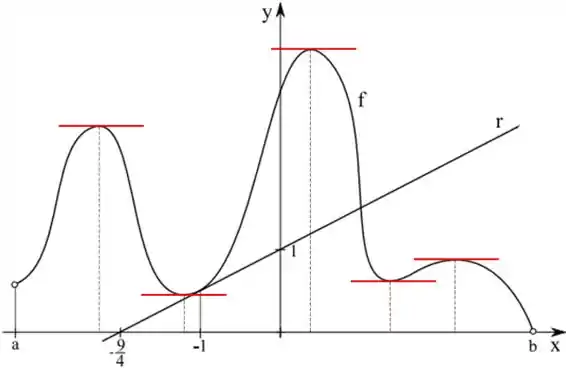
Esses sãos os pontos que que a derivada é zero.
Passo 2
Vamos indicar em um gráfico auxiliar embaixo desse onde as derivadas são positivas e negativas, mas vale lembrar que quando a derivada for positiva a função é crescente e quando a derivada for decrescente a derivada vai ser negativa. Então vamos ter
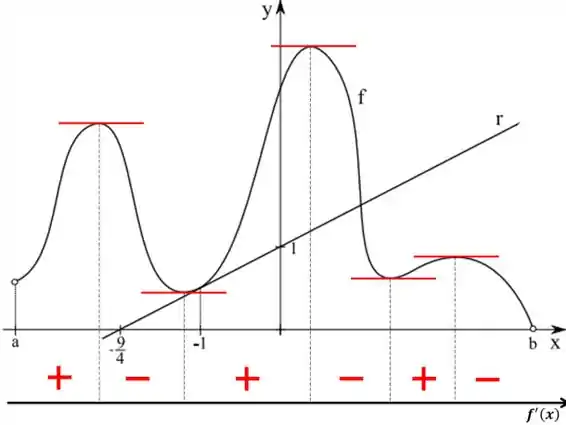
Passo 3
Para esboçarmos o gráfico da derivada temos que entender o que essa análise de sinal que fizemos antes significa.
Sempre que a derivada mudar de sinal é porque ela foi , ou seja, são as raízes da derivada, entre uma raiz e outra devemos ter um extremo relativo, isso porque para “voltar” para o eixo devemos uma hora deixar de ser crescente e passar a ser decrescente e vice versa. O esboço vai ficar algo assim
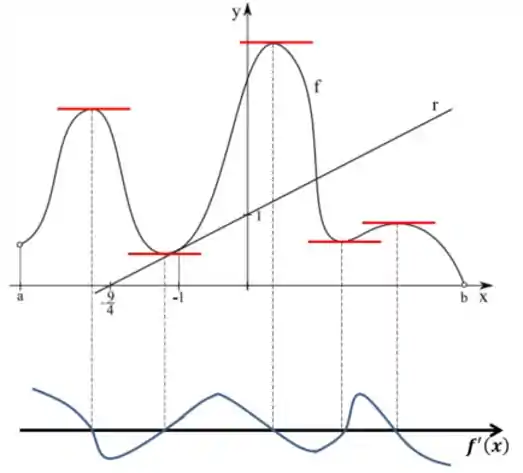
Passo 4
Para achar essa reta é um pouco complicado, não temos a sua inclinação, mas temos um ponto dela que é , outro ponto dela seria mas não sabemos , repara que temos um terceiro ponto que podemos achar, que é
A equação da reta vai ser
Multiplicando cruzado
Passo 5
A reta tangente que passa por vai ser
Multiplicando cruzado vamos ter
Comparando essa reta com a equação que achamos no passo anterior, vamos ter
Com isso já sabemos a derivada, que vai ser
Substituindo na segunda equação que achamos vamos ter