UFU, Sem Campus, Cálculo 1, Listas de Cálculo 1 - Profª Sonia Berrios - Lista 2 - Limites, Continuidade e Derivadas, Questão 36c
Encontre o limite, se existir.
c)
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente calcular o limite da função quando tende a zero pela direita, ou seja, por valores positivos.
Pra isso, nós vamos separar o limite do produto no produto dos limites:
E avaliar o que acontece com cada uma das funções quando se aproxima de zero por valores positivos.
Vamos lá!
Passo 2
Vamos começar analisando a função logaritmo natural, , dando uma olhadinha no gráfico dela:
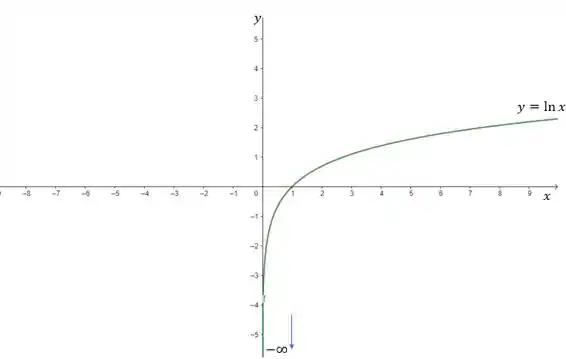
Repare que a medida que nós vamos nos aproximando de , vindo lá da direita e descendo, nossa função vai tendendo a valores negativos cada vez maiores, certo? Isso quer dizer, que ela vai pra .
Então, vamos ter:
E o quê que acontece com a função ? Bom, nós temos o ficando cada vez menorzinho e se aproximando de zero. Então, a gente tem um valor constante sendo dividido por um valor cada vez menor. Isso significa que o resultado dessa divisão vai tendendo a infinito. Mas vai tendendo a , porque temos (valores positivos). Então, vai ficar:
Logo,
Valeu, galera! Até a próxima! 😉