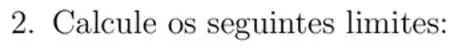
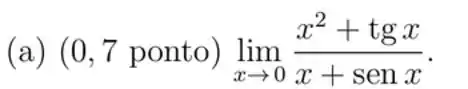
Passo 1
Substituindo esse cara aí, vai ficar:
Indeterminação de quociente, podemos aplicar L’Hospital para fugir dela!
Passo 2
Aplicamos L’Hospital aí:
Agora é só substituir o limite e acabou, lembrando que .
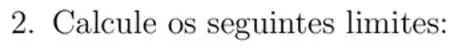
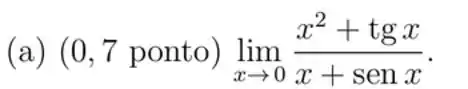
Substituindo esse cara aí, vai ficar:
Indeterminação de quociente, podemos aplicar L’Hospital para fugir dela!
Aplicamos L’Hospital aí:
Agora é só substituir o limite e acabou, lembrando que .