UFPE – Cálculo 1 – 2020.2 – Terceiro Exame – Exercício 3
Calcule o volume do sólido cuja base é o semicírculo , , e cujas secções perpendiculares ao eixo são triângulos equiláteros.
Passo 1
Fala galerinha, beleza?
Esse problema é um pouco confuso e vamos precisar ter uma boa abstração para entender o que está acontecendo, já que desenhos são difíceis de visualizar.
Primeiro fazemos um esboço no plano da base do sólido:
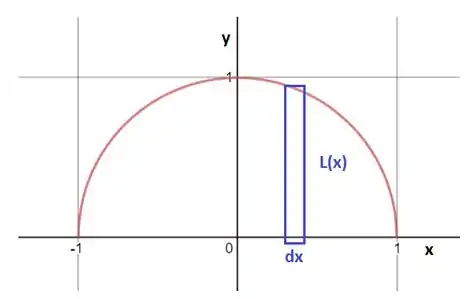
A ideia básica é a seguinte: vamos empilhar várias plaquinhas perpendiculares ao eixo . Essas plaquinhas serão triângulos equiláteros de lado e terão uma espessura infinitesimal . O volume de uma dessas plaquinhas é
Lembre-se que a área de um triângulo equilátero é
Acontece que é uma função de , como mostrado na figura:
Logo,
Portanto, o volume da plaquinha é
Passo 2
Para achar o volume do sólido completo, basta somar os volumes infinitesimais de cada plaquinha, o que corresponde a uma integral com indo de até :
Como o integrando é uma função par, podemos fazer
Agora é só fazer a integral:
Com isso, achamos o volume do sólido:
Eu sei que não é muito fácil enxergar o que está acontecendo, mas é sempre muito útil pensar nessa ideia de plaquinhas ou disquinhos empilhados 😉!