Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Cálculo de Volumes – Discos e Anéis

Ver Teoria
Exercício 142123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Cálculo de Volumes através de Integrais

Calcule o volume do sólido obtido pela rotação em torno do eixo O x do conjunto:

R = x , y ∈ R 2 0 ≤ x ≤ 2 ,   0 ≤ y ≤ 1 1 + x 2

Passo 1

Vamos começar desenhando a região R . Em primeiro lugar, eu não faço ideia como é o gráfico do 1 1 + x 2 , mas eu sei que é um termo sempre positivo, já que x 2 ≥ 0 e x 2 + 1 ≥ 1 . Com x variando de 0 até 2 , dado que o y vai do eixo x até f x = 1 1 + x 2 , sendo f 0 = 1 e f 2 = 1 5 , nosso gráfico vai ficar assim:

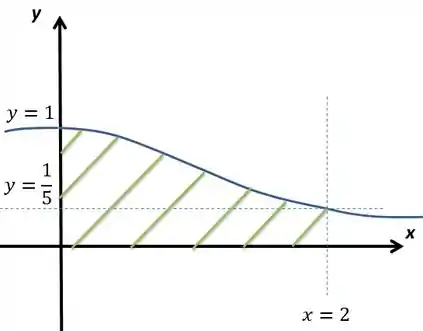
R seria essa região em verde. A questão quer que giremos em torno do eixo x essa região. Por definição, vamos calcular o volume da seguinte maneira:

V = ∫ a b π f x 2 d x

= ∫ 0 2 π 1 1 + x 2 2 d x

= π ∫ 0 2 d x 1 + x 2 2

Essa integral tem no seu denominador o formato clássico para a integral por substituição trigonométrica, vamos tentar esse método.

Passo 2

O caso da integral seria o do a 2 + x 2 , que pede a substituição x = a tg ⁡ θ , sendo que teríamos a = 1 :

x = tg ⁡ θ → d x = sec 2 ⁡ θ d θ

Devemos mudar os limites também, superior e inferior:

x s u p = 2 = tg ⁡ θ → θ = arctg ⁡ 2

x i n f = 0 = tg ⁡ θ → θ = 0

π ∫ 0 arctg ⁡ 2 d x 1 + x 2 2 = π ∫ 0 arctg ⁡ 2 sec 2 ⁡ θ d θ 1 + tg 2 ⁡ θ 2

= π ∫ 0 arctg ⁡ 2 sec 2 ⁡ θ d θ sec 2 ⁡ θ 2

= π ∫ 0 arctg ⁡ 2 d θ sec 2 ⁡ θ

= π ∫ 0 arctg ⁡ 2 cos 2 ⁡ θ d θ

Como temos a relação trigonométrica que diz que cos 2 ⁡ θ = 1 + cos ⁡ 2 θ 2 , podemos substituir na integral ficando da seguinte maneira:

π ∫ 0 arctg ⁡ 2 cos 2 ⁡ θ d θ = π ∫ 0 arctg ⁡ 2 1 + cos ⁡ 2 θ 2 d θ

= π 2 θ + sen ⁡ 2 θ 2 [ arctg ⁡ 2 0

Passo 3

Substituindo os valores dos limites agora:

π 2 arctg ⁡ 2 + sen ⁡ 2 arctg ⁡ 2 2 - π 2 0 + sen ⁡ 0 2

= π 2 arctg ⁡ 2 + sen ⁡ 2 arctg ⁡ 2 2 - π 2 0

= π 2 arctg ⁡ 2 + sen ⁡ 2 arctg ⁡ 2 2

= π 2 arctg ⁡ 2 + 2 sen ⁡ arctg ⁡ 2 cos ⁡ arctg ⁡ 2 2

Usei ali a relação que diz que sen ⁡ 2 θ = 2 sen ⁡ θ cos ⁡ θ .

Agora, nossa resposta não pode ficar com esse termo gigante sen ⁡ arctg ⁡ 2 cos ⁡ arctg ⁡ 2 . Agora, vamos desenhar um triângulo retângulo que tem um ângulo com cateto oposto valendo 2 e adjacente 1 , o que geraria tangente valendo 2 para esse ângulo:

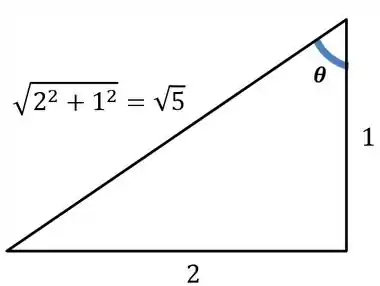
Por Pitágoras, essa hipotenusa vale 5 . Agora, o seno desse ângulo, cuja tangente é 2 , vale 2 5 , enquanto seu cosseno vale 1 5 . Assim, voltando à nossa resposta:

π 2 arctg ⁡ 2 + 2 sen ⁡ arctg ⁡ 2 cos ⁡ arctg ⁡ 2 2 = π 2 arctg ⁡ 2 + 2 2 5 1 5 2

= π 2 arctg ⁡ 2 + 2 5

Eis nossa resposta!

Resposta

V = π 2 arctg ⁡ 2 + 2 5   u . v .

Exercícios de Livros Relacionados

Determine o volume do sólido obtido com a rotação da região limitada por y = x e pelas retas y = 2 e x = 0 em torno Do eixo x .Do eixo y .Da reta y = 2 .Da reta x = 4 .
Volume de um toro. O disco x 2 + y 2 ≤ a 2 gira em torno da reta x = b ( ba ) para gerar um sólido em forma de rosquinha chamado toro. Determine seu volume. (Sugestão: ∫ - a a a 2 - y 2 d y = π a 2 /
42: A região delimitada pelas curvas dadas é girada em torno do eixo especificado. Ache o volume do sólido resultante por qualquer método. x = y - 3 2 ,x = 4 ; em torno de y = 1 .
Por integração, determine o volume do sólido obtido pela rotação da região triangular com os vértices ( 0,0 ) , b , 0 e ( 0 , h ) em torno Do eixo x .Do eixo y .