Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Cálculo de Volumes – Discos e Anéis

Ver Teoria
Exercício 491234567891011121314151617181920212223242526272829303132333435363738394041424344454647485051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Calcule o volume do sólido obtido pela rotação em torno do eixo x   da região delimitada pela curva y = x ² - x + 3 e a reta y = 3 .

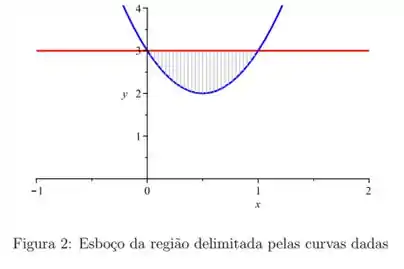
Passo 1

A rotação da área da figura em torno de um plano perpendicular ao eixo x nos dá um anel de raio externo R = 3 e raio interno r = x ² - x + 3 , de forma que a área da seção transversal é

A = π R ² - π r ²

A = π 3 ² - π ( x ² - x + 3 ) ²

A = - π ( x 4 - 2 x 3 + 7 x 2 - 6 x )

Passo 2

O sólido será limitado pelo intervalo 0,1 , então o volume é dado pela integral

∫ 0 1 A x d x

∫ 0 1 - π ( x 4 - 2 x 3 + 7 x 2 - 6 x ) d x

- π ∫ 0 1 ( x 4 - 2 x 3 + 7 x 2 - 6 x ) d x

Passo 3

Agora só falta resolver a integral.

V = - π ∫ 0 1 ( x 4 - 2 x 3 + 7 x 2 - 6 x ) d x

= - π x 5 5 - 2 x 4 4 + 7 x ³ 3 - 6 x ² 2 0 1

= - π 1 5 - 1 2 + 7 3 - 3

= 29 π 30 u . v

Resposta

29 π 30 u . v

Exercícios de Livros Relacionados

Determine o volume do sólido obtido com a rotação da região limitada por y = x e pelas retas y = 2 e x = 0 em torno Do eixo x .Do eixo y .Da reta y = 2 .Da reta x = 4 .
Volume de um toro. O disco x 2 + y 2 ≤ a 2 gira em torno da reta x = b ( ba ) para gerar um sólido em forma de rosquinha chamado toro. Determine seu volume. (Sugestão: ∫ - a a a 2 - y 2 d y = π a 2 /
42: A região delimitada pelas curvas dadas é girada em torno do eixo especificado. Ache o volume do sólido resultante por qualquer método. x = y - 3 2 ,x = 4 ; em torno de y = 1 .
Por integração, determine o volume do sólido obtido pela rotação da região triangular com os vértices ( 0,0 ) , b , 0 e ( 0 , h ) em torno Do eixo x .Do eixo y .