Cálculo de Volumes através de Integrais
Calcule o volume do sólido de revolução obtido pela rotação do semicírculo:
Em torno da reta .
Passo 1
Seguinte, vamos começar esse negócio desenhando a Região , que é uma circunferência de raio centrada na origem, porém sem a parte em que , ou seja, só um semicírculo. Vou colocar no desenho também o eixo de rotação , que é paralelo ao eixo :
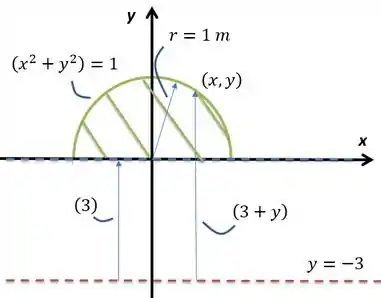
Eu deixei ali indicadas duas setas, ambas partindo do eixo de rotação. Quando rotacionarmos a região é como se fizéssemos o volume gerado na rotação do gráfico verde menos aquele gerado pelo tracejado azul, que coloquei em cima do eixo . Basicamente, para rodar a região em torno de determinado eixo temos que rodar a linha que delimita superiormente a região menos a rotação daquela que delimita inferiormente, sendo que no caso a verde está por cima e a azul por baixo. Os respectivos raios de rotação de cada uma são e , onde pode ser achado sendo isolado na equação do círculo:
Dessa forma, o volume da rotação de em torno de será dado pelo método das seções transversais, visualizando ainda que os limites de integração para nessa figura vão de a , ou seja, de até :
Passo 2
Resolvendo a integral:
A primeira integral pode ser feita por substituição trigonométrica, sendo que esse seria o caso da substituição por um .
Nesse intervalo, . Ficamos com a integral de , porém tem uma relação trigonométrica muito útil para integrar esse cara:
Passo 3
A outra integral sai direto pela integral do polinômio:
Assim, somando os resultados das duas integrais, temos: